题目内容
已知集合S={a1,a2},T={b1,b2},则从集合S到T的映射共有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
分析:由映射的定义知集合A中每一个元素在集合B中有唯一的元素和它对应,A中a1在集合B中有b1或b2与a1对应,有两种选择,同理集合A中a2也有两种选择,由分步乘法原理求解即可.
解答:解:由映射的定义知A中a1在集合B中有b1或b2与a1对应,有两种选择,
同理集合A中a2也有两种选择,
由分步乘法原理得从集合A={a1,a2},到集合B={b1,b2}的不同映射共有2×2=4个
故选D.
同理集合A中a2也有两种选择,
由分步乘法原理得从集合A={a1,a2},到集合B={b1,b2}的不同映射共有2×2=4个
故选D.
点评:本题考查映射的定义和个数计算、乘法原理,正确把握映射的定义是解题的关键.

练习册系列答案
相关题目
 A,则称集合A具有性质P。
A,则称集合A具有性质P。 ;
;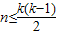 ;
; ;
;