题目内容
(本小题共12分)
 在三棱柱ABC—A1B1C1中,底面是边长为
在三棱柱ABC—A1B1C1中,底面是边长为![]() 的正三角形,点A1在底面ABC上的射影O恰是BC的中点.
的正三角形,点A1在底面ABC上的射影O恰是BC的中点.
(1)求证:面A1AO![]() 面BCC1B1;
面BCC1B1;
(2)当AA1与底面成45°角时,求二面角A1—AC—B的大小;
(3)若D为侧棱AA1上一点,当![]() 为何值时,BD⊥A1C1.
为何值时,BD⊥A1C1.
arctan2,![]()
解析:
 证明:(1)连AO, ∵⊿ABC为正三角形, ∴AO⊥BC.
证明:(1)连AO, ∵⊿ABC为正三角形, ∴AO⊥BC.
又∵A1O⊥面ABC,∴A1O⊥BC,∴BC⊥面A1AO
∴面A1AO⊥面BCC1B1 ………4分
(2)过O作OE⊥AC于E,连A1E,
∵A1O⊥面ABC,
∴![]() ,∴∠A1EO即为所求的平面角.
,∴∠A1EO即为所求的平面角.
∵正⊿ABC的边长为![]() ,∠A1AO=45°,
,∠A1AO=45°,
∴![]() .
.

∴二面角A1—AC—B的大小为arctan2 . …………8分
(3)过D作DF//A1O交AO于F,则DF⊥面ABC,
连BF,要使BD⊥A1C1,只要使BF⊥AC,
∵⊿ABC为正三角形,
∴只要F为△ABC的中心即可,
∴![]() 时,BD⊥A1C1 . …………12分
时,BD⊥A1C1 . …………12分

练习册系列答案
相关题目
 ⊥平面
⊥平面 ,
, ∥
∥ 是正三角形,
是正三角形, ,且
,且 是
是 的中点
的中点
 ∥平面
∥平面 ;
; .
. 名,女同学有
名,女同学有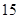 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个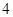 人的课外兴趣小组.
人的课外兴趣小组. 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;


 ,
, ,求证:
,求证: .
. 的值.
的值.