题目内容
已知函数f(x)=ln|x|(x≠0),函数g(x)=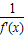 +af'(x)(x≠0)
+af'(x)(x≠0)(1)当x≠0时,求函数y=g(x)的表达式;
(2)若a>0,函数y=g(x)在(0,+∞)上的最小值是2,求a的值;
(3)在(2)的条件下,求直线y=
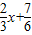 与函数y=g(x)的图象所围成图形的面积.
与函数y=g(x)的图象所围成图形的面积.
【答案】分析:(1)分情况讨论x的取值化简绝对值,求出f′(x)得到x>0和x<0导函数相等,代入到g(x)中得到即可;
(2)根据基本不等式得到g(x)的最小值即可求出a;
(3)先联立直线与函数解析式求出交点,利用定积分求直线和函数图象围成面积的方法求出即可.
解答:解:(1)∵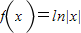 ,
,
∴当x>0时,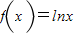 ;当x<0时,
;当x<0时,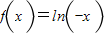
∴当x>0时,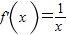 ;当x<0时,
;当x<0时,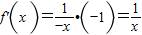 .
.
∴当x≠0时,函数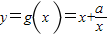 .
.
(2)∵由(1)知当x>0时,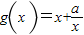 ,
,
∴当a>0,x>0时,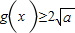 当且仅当
当且仅当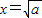 时取等号.
时取等号.
∴函数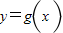 在
在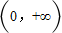 上的最小值是
上的最小值是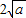 ,∴依题意得
,∴依题意得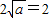 ∴a=1.
∴a=1.
(3)由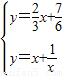 解得
解得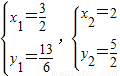
∴直线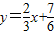 与函数
与函数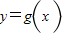 的图象所围成图形的面积
的图象所围成图形的面积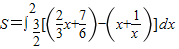 =
=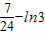
点评:考查学生导数运算的能力,理解函数最值及几何意义的能力,利用定积分求平面图形面积的能力.
(2)根据基本不等式得到g(x)的最小值即可求出a;
(3)先联立直线与函数解析式求出交点,利用定积分求直线和函数图象围成面积的方法求出即可.
解答:解:(1)∵
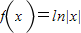 ,
,∴当x>0时,
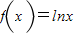 ;当x<0时,
;当x<0时,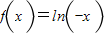
∴当x>0时,
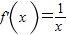 ;当x<0时,
;当x<0时,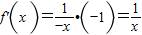 .
.∴当x≠0时,函数
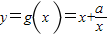 .
.(2)∵由(1)知当x>0时,
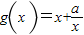 ,
,∴当a>0,x>0时,
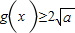 当且仅当
当且仅当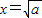 时取等号.
时取等号.∴函数
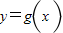 在
在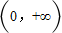 上的最小值是
上的最小值是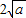 ,∴依题意得
,∴依题意得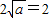 ∴a=1.
∴a=1.(3)由
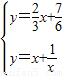 解得
解得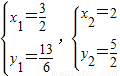
∴直线
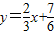 与函数
与函数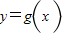 的图象所围成图形的面积
的图象所围成图形的面积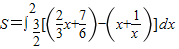 =
=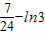
点评:考查学生导数运算的能力,理解函数最值及几何意义的能力,利用定积分求平面图形面积的能力.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目