题目内容
正数数列{an}的前n项和Sn,满足4Sn=(an+1)2,试求:(1)数列{an}的通项公式;
(2)设bn=
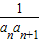 ,数列的前n项的和为Bn,求证:Bn<
,数列的前n项的和为Bn,求证:Bn< ;
;(3)设cn=an•(
 )n,求数列{cn}的前n项和Tn.
)n,求数列{cn}的前n项和Tn.
【答案】分析:(1)由4Sn=(an+1)2,利用迭代法能求出an=2n-1.
(2)由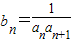 =
=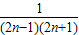 =
=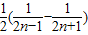 ,利用裂项求和法能够证明Bn<
,利用裂项求和法能够证明Bn< .
.
(3)由an=2n-1,知cn=an•( )n=(2n-1)•(
)n=(2n-1)•( )n,利用错位相减法能够求出数列{cn}的前n项和Tn.
)n,利用错位相减法能够求出数列{cn}的前n项和Tn.
解答:解:(1)∵4Sn=(an+1)2,
∴4Sn-1=(an-1+1)2,n≥2,
作差,得4(Sn-Sn-1)=(an+1)2-(an-1+1)2,
∴4an=(an+an-1+2)(an-an-1),
整理,得(an+an-1)(an-an-1-2)=0.
∵{an}正数数列,∴an-an-1=2,
由2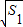 =a1+1,得a1=1,
=a1+1,得a1=1,
∴an=2n-1.…(4分)
(2)∵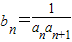 =
=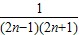 =
=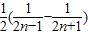 ,
,
∴数列的前n项的和
Bn=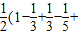 …+
…+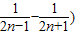
=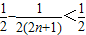 ,
,
故Bn< .…(9分)
.…(9分)
(3)∵an=2n-1,
∴cn=an•( )n=(2n-1)•(
)n=(2n-1)•( )n,
)n,
∴Tn=c1+c2+c3+…+cn
=1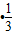 +3•
+3•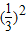 +5•(
+5•( )3+…+(2n-3)•(
)3+…+(2n-3)•( )n-1+(2n-1)•(
)n-1+(2n-1)•( )n,
)n,
 Tn=1•
Tn=1•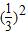 +3•(
+3•( )3+5•(
)3+5•( )4…+(2n-3)•(
)4…+(2n-3)•( )n+(2n-1)•(
)n+(2n-1)•( )n+1,
)n+1,
∴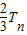 =
= +2•(
+2•( )2+2•(
)2+2•( )3+2•(
)3+2•( )4+…+2•(
)4+…+2•( )n-(2n-1)•(
)n-(2n-1)•( )n+1
)n+1
=2×[ +(
+( )2+(
)2+( )3+(
)3+( )4+…+(
)4+…+( )n]-
)n]- -(2n-1)•(
-(2n-1)•( )n+1
)n+1
=2×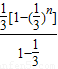 -
- -(2n-1)•(
-(2n-1)•( )n+1
)n+1
=1-( )n-
)n- -(2n-1)•(
-(2n-1)•( )n+1
)n+1
= -(
-( )n-(2n-1)•(
)n-(2n-1)•( )n+1,
)n+1,
∴Tn=1-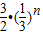 -(2n-1)
-(2n-1)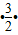 (
( )n+1=1-
)n+1=1-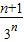 .
.
点评:本题考查数列的通项公式的求法,考查不等式的证明,考查数列的前n项和的求法,解题时要认真审题,注意迭代法、裂项求和法、错位相减法的合理运用.
(2)由
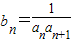 =
=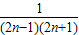 =
=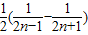 ,利用裂项求和法能够证明Bn<
,利用裂项求和法能够证明Bn< .
.(3)由an=2n-1,知cn=an•(
 )n=(2n-1)•(
)n=(2n-1)•( )n,利用错位相减法能够求出数列{cn}的前n项和Tn.
)n,利用错位相减法能够求出数列{cn}的前n项和Tn.解答:解:(1)∵4Sn=(an+1)2,
∴4Sn-1=(an-1+1)2,n≥2,
作差,得4(Sn-Sn-1)=(an+1)2-(an-1+1)2,
∴4an=(an+an-1+2)(an-an-1),
整理,得(an+an-1)(an-an-1-2)=0.
∵{an}正数数列,∴an-an-1=2,
由2
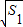 =a1+1,得a1=1,
=a1+1,得a1=1,∴an=2n-1.…(4分)
(2)∵
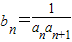 =
=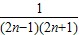 =
=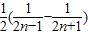 ,
,∴数列的前n项的和
Bn=
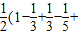 …+
…+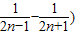
=
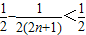 ,
,故Bn<
 .…(9分)
.…(9分)(3)∵an=2n-1,
∴cn=an•(
 )n=(2n-1)•(
)n=(2n-1)•( )n,
)n,∴Tn=c1+c2+c3+…+cn
=1
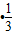 +3•
+3•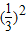 +5•(
+5•( )3+…+(2n-3)•(
)3+…+(2n-3)•( )n-1+(2n-1)•(
)n-1+(2n-1)•( )n,
)n, Tn=1•
Tn=1•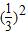 +3•(
+3•( )3+5•(
)3+5•( )4…+(2n-3)•(
)4…+(2n-3)•( )n+(2n-1)•(
)n+(2n-1)•( )n+1,
)n+1,∴
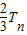 =
= +2•(
+2•( )2+2•(
)2+2•( )3+2•(
)3+2•( )4+…+2•(
)4+…+2•( )n-(2n-1)•(
)n-(2n-1)•( )n+1
)n+1=2×[
 +(
+( )2+(
)2+( )3+(
)3+( )4+…+(
)4+…+( )n]-
)n]- -(2n-1)•(
-(2n-1)•( )n+1
)n+1=2×
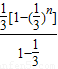 -
- -(2n-1)•(
-(2n-1)•( )n+1
)n+1=1-(
 )n-
)n- -(2n-1)•(
-(2n-1)•( )n+1
)n+1=
 -(
-( )n-(2n-1)•(
)n-(2n-1)•( )n+1,
)n+1,∴Tn=1-
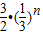 -(2n-1)
-(2n-1)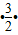 (
( )n+1=1-
)n+1=1-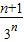 .
.点评:本题考查数列的通项公式的求法,考查不等式的证明,考查数列的前n项和的求法,解题时要认真审题,注意迭代法、裂项求和法、错位相减法的合理运用.

练习册系列答案
相关题目