题目内容
设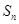 为等差数列
为等差数列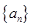 的前
的前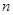 项和,
项和,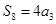 ,
,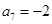 ,则
,则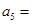 ( )
( )
A.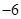 | B.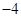 | C.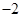 | D. |
D.
解析试题分析:∵等差数列 ,
,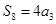 ,∴
,∴ ,
,
又∵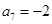 ,∴
,∴ ,联立方程,可得
,联立方程,可得 ,
, ,∴
,∴ .
.
考点:等差数列的通项公式及其前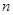 项和.
项和.

练习册系列答案
相关题目
已知在等差数列 中,
中, 的等差中项为
的等差中项为 ,
,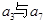 的等差中项为
的等差中项为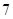 ,则数列
,则数列 的通项公式
的通项公式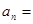 ( )
( )
A. | B. -1 -1 | C. +1 +1 | D. -3 -3 |
已知数列 为等差数列,
为等差数列, 公差
公差 ,
, 、
、 、
、 成等比,则
成等比,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知等差数列 的首项
的首项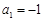 ,公差
,公差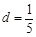 ,则
,则 的第一个正数项是( )
的第一个正数项是( )
A.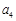 | B.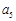 | C.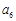 | D.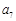 |
已知等比数列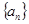 中,各项都是正数,且
中,各项都是正数,且 成等差数列,则
成等差数列,则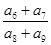 等于( )
等于( )
A.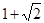 | B.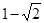 | C.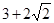 | D. |
已知数列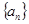 为等差数列,若
为等差数列,若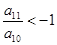 ,且它们的前n项和
,且它们的前n项和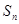 有最大值,
有最大值,
则使得 的n的最大值为( ).
的n的最大值为( ).
| A.11 | B.19 | C.20 | D.21 |
已知数列 ,若
,若 ,记
,记 为
为 的前
的前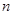 项和,则使
项和,则使 达到最大的
达到最大的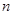 值为( )
值为( )
| A.13 | B.12 | C.11 | D.10 |
等差数列 的值为( )
的值为( )
| A.66 | B.99 | C.144 | D.297 |
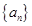 的各项都是正数,且对任意
的各项都是正数,且对任意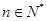 都有
都有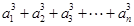
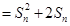 ,其中
,其中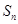 为数列
为数列 项和.
项和.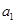 、
、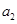 ;
;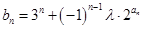 ,对任意的
,对任意的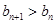 恒成立,求实数
恒成立,求实数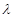 的取值范围.
的取值范围.