题目内容
已知等比数列{an}中an+1>an,且a3+a7=3,a2•a8=2,则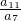
- A.

- B.

- C.

- D.2
D
分析:利用等比数列的性质,由a2•a8=2,得到a3•a7=2,与a3+a7=3联立,再根据数列是递增数列,求出a3与a7的值,进而利用等比数列的通项公式分别表示出a3与a7,并求出a3与a7的比值,得到q4的值,最后把所求的式子利用等比数列的通项公式变形后,将q4代入即可求出值.
解答:∵等比数列{an}中an+1>an,即数列为递增数列,a3+a7=3,a2•a8=2,
∴ ,
,
解得a3=1,a7=2,
∴ =
= ,
,
∴q4=2,
∴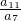 =
= .
.
故选D
点评:此题考查了等比数列的性质,以及等比数列的通项公式,熟练掌握性质与公式是解本题的关键.
分析:利用等比数列的性质,由a2•a8=2,得到a3•a7=2,与a3+a7=3联立,再根据数列是递增数列,求出a3与a7的值,进而利用等比数列的通项公式分别表示出a3与a7,并求出a3与a7的比值,得到q4的值,最后把所求的式子利用等比数列的通项公式变形后,将q4代入即可求出值.
解答:∵等比数列{an}中an+1>an,即数列为递增数列,a3+a7=3,a2•a8=2,
∴
 ,
,解得a3=1,a7=2,
∴
 =
= ,
,∴q4=2,
∴
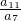 =
= .
.故选D
点评:此题考查了等比数列的性质,以及等比数列的通项公式,熟练掌握性质与公式是解本题的关键.

练习册系列答案
相关题目