题目内容
如图1-1-2,在四边形ABCD中，BC=m,DC=2m,四个内角A、B、C、D之比为3∶7∶4∶10,试求四边形ABCD的面积.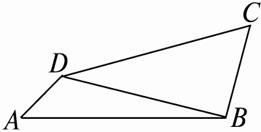
图1-1-2
解:由题意知,设四个内角A,B,C,D的大小依次为3x,7x,4x,10x,则3x+7x+4x+10x=360°.得x=15°，即A=45°，B=105°，C=60°，D=150°,在△BCD中,由余弦定理,得
BD2=BC2+DC2-2BC·DC·cosC=m2+(2m)2-2×m×2m×cos60°=3m2,
∴BD=
m.
∴S△BCD=
DC·BC·sinC=
×m×2m×
=
m2.
在△BCD中,BD2+BC2=DC2，∴∠DBC=90°.∴∠BDC=30°.
在△BAD中,由正弦定理,得
AB=
=
m.
又∠ABD=105°-90°=15°,
∴S△ABD=
AB·BD·sin15°=
×
m×
m×
=
m2.
∴S四边形ABCD=S△ABD+S△BCD=
m2+
m2=
m2.
练习册系列答案
相关题目
（2012•广东）如图所示，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点E在线段PC上，PC⊥平面BDE．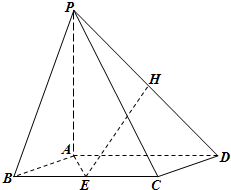
如图所示，在四棱锥P-ABCD中，底面ABCD为菱形，且AB=2，PA⊥平面ABCD，∠ABC=60°，E是BC的中点．
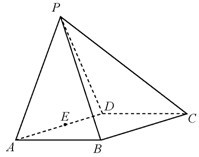（2013•哈尔滨一模）如图所示，在四棱锥P-ABCD中，四边形ABCD为菱形，△PAD为等边三角形，平面 PAD⊥平面ABCD，∠DAB=60°，AB=2且，E为AD 的中点．