题目内容
用数学归纳法证明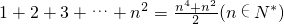 的过程中,由n=k变到n=k+1时,左边总共增加了________ 项.
的过程中,由n=k变到n=k+1时,左边总共增加了________ 项.
2k+1
分析:根据等式1+2+3+…+n2=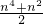 ,考虑n=k和n=k+1时,等式左边的项,再把n=k+1时等式的左端减去n=k时等式的左端,即可得到答案.
,考虑n=k和n=k+1时,等式左边的项,再把n=k+1时等式的左端减去n=k时等式的左端,即可得到答案.
解答:当n=k时,等式左端=1+2++k2,
当n=k+1时,等式左端=1+2++k2+(k2+1)+(k2+2)+(k2+3)+…+(k+1)2,
所以增加的项数为:(k+1)2-(k2+1)+1=2k+1
即增加了2k+1项.
故答案为:2k+1.
点评:此题主要考查数学归纳法的问题,解答的关键是明白等式左边项的特点,再把n=k+1时等式的左端减去n=k时等式的左端.
分析:根据等式1+2+3+…+n2=
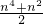 ,考虑n=k和n=k+1时,等式左边的项,再把n=k+1时等式的左端减去n=k时等式的左端,即可得到答案.
,考虑n=k和n=k+1时,等式左边的项,再把n=k+1时等式的左端减去n=k时等式的左端,即可得到答案.解答:当n=k时,等式左端=1+2++k2,
当n=k+1时,等式左端=1+2++k2+(k2+1)+(k2+2)+(k2+3)+…+(k+1)2,
所以增加的项数为:(k+1)2-(k2+1)+1=2k+1
即增加了2k+1项.
故答案为:2k+1.
点评:此题主要考查数学归纳法的问题,解答的关键是明白等式左边项的特点,再把n=k+1时等式的左端减去n=k时等式的左端.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
用数学归纳法证明不等式“
+
+…+
>
(n>2)”时的过程中,由n=k到n=k+1时,不等式的左边( )
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
| 13 |
| 24 |
A、增加了一项
| ||||||
B、增加了两项
| ||||||
C、增加了两项
| ||||||
D、增加了一项
|

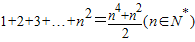 的过程中,由n=k变到n=k+1时,左边总共增加了 项.
的过程中,由n=k变到n=k+1时,左边总共增加了 项.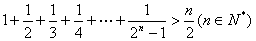 的过程中,由“
的过程中,由“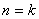 ”成立递推到“
”成立递推到“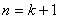 ”时不等式左端增加的项数为 ( )
”时不等式左端增加的项数为 ( )