题目内容
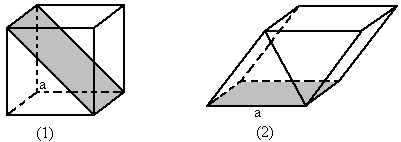
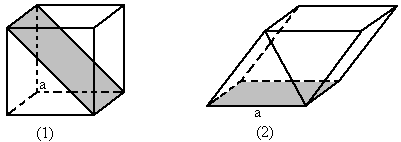
已知如图几何体,正方形 和矩形
和矩形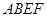 所在平面互相垂
所在平面互相垂
直,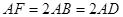 ,
,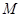 为
为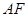 的中点,
的中点,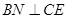 。
。
(Ⅰ)求证: 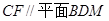 ;
;
(Ⅱ)求二面角 的大小。
的大小。

【答案】
(I)证明:连结 交
交 于
于 ,连结
,连结
因为 为
为 中点,
中点, 为
为 中点,
中点,
所以 ,
,
又因为 ,
,
所以 ;
…………………4分
;
…………………4分
(II)因为正方形 和矩形
和矩形 所在平面互相垂直,
所在平面互相垂直,
所以
以 为原点,以
为原点,以 为
为 轴建立空间直角坐标系,如图取
轴建立空间直角坐标系,如图取 =1
=1
 ,
, ,
, ,
, ,
,
设平面 的法向量为
的法向量为 = (x ,y , z
),
= (x ,y , z
),

 ……6分
……6分
设平面 的法向量为
的法向量为 = (x ,y , z
),
= (x ,y , z
),


 …………………8分
…………………8分

所以二面角 的大小为
的大小为 。
。

【解析】略

练习册系列答案
相关题目