Question

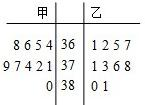某学校问了预防甲流感，每天都对同学进行体温抽查，某一天，随机抽取甲，乙两个班级各10名同学，测量他们的体温如下图（单位0.1摄氏度）
（1）计算甲班和乙班的平均温度，并比较哪个班偏高；
（2）现在从甲班这10人中随机抽取两名体温不低于37摄氏度的同学，求体温为38摄氏度的同学被抽到的概率．
（3）若人的体温在[36.5，37.7]时是正常的，如果高出正常体温，就要送到专门的发热门诊就诊，以此样本为基础，测算一下，全校1000人，恰有10人送发热门诊的概率．（只保留计算式子，不要求计算）

Answer 1

分析：（1）依据平均数的定义，分别求出甲班和乙班的学生的平均温度，从而得出结论．
（2）甲班10名同学中，体温不低于37摄氏度的有6人，其中体温不小于38度得有2人，要抽取两个人，所求的概率是P=

C 1 5

C 2 6

=

1

3

．
（3）在样本中高出正常体温的学生是5个人，所以每个学生体温高出正常体温的概率为

5

20

=

1

4

，要求的是

C

1000 10

(

1

4

)10(1-

1

4

)990．

解答：解：（1）

.

x

甲=

36.4+36.5+36.6+36.8+37.1+37.2+37.4+37.7+37.9+38.0

10

=37.16，同理算出

.

x

乙=37.14，所以甲稍高些．
（2）甲班10名同学中，体温不低于37摄氏度的有6人，其中体温不小于38度得有2人，故所求的概率是P=

C 1 5

C 2 6

=

1

3

．
（3）在样本中高出正常体温的学生是5个人，所以整个比例是

5

20

=

1

4

．
可以估计此学校每个学生体温高出正常体温的概率是

1

4

，1000人相当于独立重复试验，要求的是

C

10 1000

(

1

4

)10(1-

1

4

)990=

C

10 1000

3990

41000

．

点评：本题考查用样本估计总体，n次独立重复试验恰好发生K次得概率，求出学校每个学生体温高出正常体温的概率，是解题的关键．