题目内容
16.在直角三角形ABC中,AB=AC=3,$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{2}{3}$$\overrightarrow{AC}$.设BF与CE交点为P,则$\overrightarrow{AP}•\overrightarrow{EF}$的值为3.分析 由条件可得$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,$\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{AC}$-$\frac{1}{3}$$\overrightarrow{AB}$.设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,根据$\overrightarrow{FP}$∥$\overrightarrow{FB}$,求得y=$\frac{2}{3}$(1-x) ①.由$\overrightarrow{CP}$∥$\overrightarrow{CE}$,求得y=1-3x ②.由①②求得x、y的值,可得$\overrightarrow{AP}$═$\frac{1}{7}$$\overrightarrow{AB}$+$\frac{4}{7}$$\overrightarrow{AC}$.再利用两个向量数量积的运算法则求得$\overrightarrow{AP}•\overrightarrow{EF}$ 的值.
解答 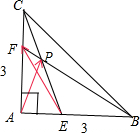 解:直角三角形ABC中,∵AB=AC=3,$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{2}{3}$$\overrightarrow{AC}$,BF与CE交点为P,
解:直角三角形ABC中,∵AB=AC=3,$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{2}{3}$$\overrightarrow{AC}$,BF与CE交点为P,
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,$\overrightarrow{EF}$=$\overrightarrow{AF}$-$\overrightarrow{AE}$=$\frac{2}{3}$$\overrightarrow{AC}$-$\frac{1}{3}$$\overrightarrow{AB}$.
设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则$\overrightarrow{FP}$=$\overrightarrow{AP}$-$\overrightarrow{AF}$=x$\overrightarrow{AB}$+(y-$\frac{2}{3}$)$\overrightarrow{AC}$,$\overrightarrow{FB}$=$\overrightarrow{AB}$-$\overrightarrow{AF}$=$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$.
再根据$\overrightarrow{FP}$∥$\overrightarrow{FB}$,可得$\frac{x}{1}$=$\frac{y-\frac{2}{3}}{-\frac{2}{3}}$,求得y=$\frac{2}{3}$(1-x) ①.
同理,由$\overrightarrow{CP}$∥$\overrightarrow{CE}$,求得y=1-3x ②.
由①②求得 x=$\frac{1}{7}$,y=$\frac{4}{7}$,∴$\overrightarrow{AP}$=$\frac{1}{7}$$\overrightarrow{AB}$+$\frac{4}{7}$$\overrightarrow{AC}$,
$\overrightarrow{AP}•\overrightarrow{EF}$=($\frac{1}{7}$$\overrightarrow{AB}$+$\frac{4}{7}$$\overrightarrow{AC}$ )•($\frac{2}{3}$$\overrightarrow{AC}$-$\frac{1}{3}$$\overrightarrow{AB}$ )=-$\frac{1}{21}$${\overrightarrow{AB}}^{2}$+$\frac{8}{21}$${\overrightarrow{AC}}^{2}$-$\frac{2}{21}$$\overrightarrow{AB}•\overrightarrow{AC}$
=-$\frac{1}{21}$×9+$\frac{8}{21}$×9-0=3,
故答案为:3.
点评 本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量共线的性质,两个向量数量积的运算,体现了转化、数形结合的数学思想,属于中档题.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案| A. | $\sqrt{2}$ | B. | $\sqrt{2}$或$-\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | 0 |
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{5}$ |
| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m⊥α,n⊥α,则m∥n | C. | 若α∥γ,β∥γ,则α∥β | D. | 若α⊥γ,β⊥γ,则α∥β |
| A. | 2 | B. | $\sqrt{3}$ | C. | 3 | D. | 2$\sqrt{3}$ |
| A. | $f({-\frac{1}{2}})<f({\frac{3}{4}})<f({\frac{2}{3}})$ | B. | $f({-\frac{1}{2}})<f({\frac{2}{3}})<f({\frac{3}{4}})$ | C. | $f({\frac{3}{4}})<f({\frac{2}{3}})<f({-\frac{1}{2}})$ | D. | $f({\frac{2}{3}})<f({-\frac{1}{2}})<f({\frac{3}{4}})$ |
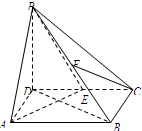 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别为CD,PB的中点.求证:
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别为CD,PB的中点.求证: