题目内容
(2013•未央区三模)若数列{an}满足a1=15,且3an+1=3an-2,则使akak+1<0的k值为( )
分析:利用3an+1=3an-2,可得an+1-an=-
,从而数列{an}是首项为15,公差为-
的等差数列,求出数列的通项,确定其正数项,即可得到结论.
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:因为3an+1=3an-2,所以an+1-an=-
,
所以数列{an}是首项为15,公差为-
的等差数列,所以an=-
n+
,
由an=-
n+
>0,得n<23.5,所以使akak+1<0的k值为23
故选D.
| 2 |
| 3 |
所以数列{an}是首项为15,公差为-
| 2 |
| 3 |
| 2 |
| 3 |
| 47 |
| 3 |
由an=-
| 2 |
| 3 |
| 47 |
| 3 |
故选D.
点评:本题考查等差数列的判定,考查数列的通项,考查学生的计算能力,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
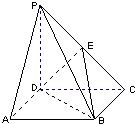 (2013•未央区三模)如图,四棱锥P-ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(2013•未央区三模)如图,四棱锥P-ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点. (2013•未央区三模)某三棱锥的三视图如图所示,该三棱锥的体积是为( )
(2013•未央区三模)某三棱锥的三视图如图所示,该三棱锥的体积是为( )