Question

已知点A(1,0),点B(2,0).

(1)若动点M满足·+||=0,求点M的轨迹C;

(2)若过点B的直线L₂(斜率不等于零)与(1)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.

Answer 1

解:(1)设M(x,y),则=(1,0),=(x-2,y),=(x-1,y),

由·+2||=0得(x-2)+y·0+2·=0.整理,得+y²=1.

∴动点M的轨迹C为以原点为中心,焦点在x轴上,长轴长为2,短轴长为2的椭圆.

(2)如图,由题意知直线L₂的斜率存在且不为零,设L₂方程为y=k(x-2)(k≠0),①

将①代入+y²=1,整理,得(2k²+1)x²-8k²·x+(8k²-2)=0,

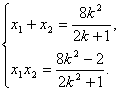由Δ＞0得0＜k²＜.设E(x₁,y₁),F(x₂,y₂),则②

令λ=,则λ=,由此可得=λ·,λ=,且0＜λ＜1.

由②知(x₁-2)+(x₂-2)=,(x₁-2)·(x₂-2)=x₁x₂-2(x₁+x₂)+4=.

∴=,即k²=.

∵0＜k²＜,∴0＜＜,解得3-2＜λ＜3+2.

又∵0＜λ＜1,∴3-2＜λ＜1.∴△OBE与△OBF面积之比的取值范围是(3-2,1).