Question

已知集合M={（x，y）|x+y≤8，x≥0，y≥0}，N={（x，y）|x-3y≥0，x≤6，y≥0}，若向区域M内随机投一点P，则点P落入区域N内的概率为（　　）

• A、

  1

  3

• B、

  1

  2

• C、

  3

  8

• D、

  3

  16

Answer 1

分析：我们分别作出集合M所表示的平面区域，即满足条件x+y≤8，x≥0，y≥0的可行域，并求出其面积用来表示全部基本事件，再求出N所表示的平面区域，即满足条件x-3y≥0，x≤6，y≥0的可行域，并求出其面积，代入几何概型公式，即可求解．

解答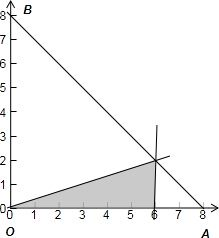：解：满足条件M={（x，y）|x+y≤8，x≥0，y≥0}的平面区域如下图中△OAB所示：其中满足条件N={（x，y）|x-3y≥0，x≤6，y≥0}的平面区域如图中阴影部分所示，
则向区域M内随机投一点P，则点P落入区域N内的概率
P=

S阴影

SOAB

=

1 2 ×6×2

1 2 ×8×8

=

3

16

故选D

点评：本题考查的知识点是几何概型，几何概型解题步骤为：求出满足条件A的基本事件对应的平面区域面积N（A），再求出总的基本事件对应平面区域面积N，最后根据P=

N(A)

N

求解．