题目内容
【题目】已知抛物线C:x2=2py经过点(2,1).
(Ⅰ)求抛物线C的方程及其准线方程;
(Ⅱ)设O为原点,过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M,N,直线y=1分别交直线OM,ON于点A和点B.求证:以AB为直径的圆经过y轴上的两个定点.
【答案】(Ⅰ) ![]() ,
,![]() ;
;
(Ⅱ)见解析.
【解析】
(Ⅰ)由题意结合点的坐标可得抛物线方程,进一步可得准线方程;
(Ⅱ)联立准线方程和抛物线方程,结合韦达定理可得圆心坐标和圆的半径,从而确定圆的方程,最后令x=0即可证得题中的结论.
(Ⅰ)将点![]() 代入抛物线方程:
代入抛物线方程:![]() 可得:
可得:![]() ,
,
故抛物线方程为:![]() ,其准线方程为:
,其准线方程为:![]() .
.
(Ⅱ)很明显直线![]() 的斜率存在,焦点坐标为
的斜率存在,焦点坐标为![]() ,
,
设直线方程为![]() ,与抛物线方程
,与抛物线方程![]() 联立可得:
联立可得:![]() .
.
故:![]() .
.
设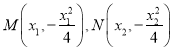 ,则
,则![]() ,
,
直线![]() 的方程为
的方程为![]() ,与
,与![]() 联立可得:
联立可得: ,同理可得
,同理可得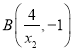 ,
,
易知以AB为直径的圆的圆心坐标为: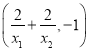 ,圆的半径为:
,圆的半径为: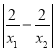 ,
,
且:![]() ,
,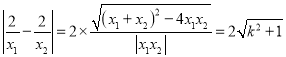 ,
,
则圆的方程为:![]() ,
,
令![]() 整理可得:
整理可得:![]() ,解得:
,解得:![]() ,
,
即以AB为直径的圆经过y轴上的两个定点![]() .
.

练习册系列答案
相关题目