Question

【题目】已知向量 =（1，3cosα）， =（1，4tanα）， ，且 =5．
（1）求| + |；
（2）设向量 与 的夹角为β，求tan（α+β）的值．

Answer 1

【答案】
（1）解：由 =（1，3cosα）， =（1，4tanα），

则 =1+12cosαtanα=5，解得 ，

因为 ，所以 ， ．

则 =（1，2 ）， =（1， ）

则 = ，

即有| |= = ；

（2）解：由（1）知 =（1，2 ）， =（1， ），

则cosβ=cos＜ ＞= = ，

即有 ，所以 ，

所以

【解析】（1）由向量的数量积的坐标公式化简即得sinα，由同角公式，求得cosα，tanα，得到向量m，n，再由模的公式即可得到所求的值；（2）运用向量的夹角公式，求得cosβ，进而得到sinβ，tanβ，再由两角和的正切公式，即可得到所求的值．
【考点精析】利用数量积表示两个向量的夹角和两角和与差的正切公式对题目进行判断即可得到答案，需要熟知设、都是非零向量，，，是与的夹角，则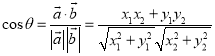；两角和与差的正切公式：．