题目内容
已知定义在实数集上的函数fn（x）=xn，n∈N*，其导函数记为fn′（x），且满足：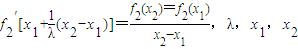
为常数．（I）试求λ的值；
（II）设函数f2n-1（x）与fn（1-x）的乘积为函数F（x），求F（x）的极大值与极小值；
（III）若gn（x）=ex•fn（x），试证明关于x的方程
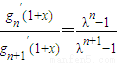在区间（0，2）上有唯一实数根；记此实数根为x（n），求x（n）的最大值．
【答案】分析：（1）利用求导公式求函数的导数，令n=2，代入等式求λ，
（2）利用导数公式求函数的导数，画图求函数的单调性，根据导数求极值，
（3）利用导数求导和利用数学归纳法，在当a=1时和当a≥2时的条件下证明
解答：解：（1）f′2（x）=2x，∴2[x1+
（x2-x1）]=（x22-x12）/（x2-x1）
∴x2+x1=2x1+
（x2-x1）⇒λ=2
（2）令y=F（X）=f′2n-1（x）•fn（1-x）=（1-x）n•x2n-1，则
①当n=1时，y=x-x2，y′=1-2x，令y′=o，得x=
，x∈{-∞，
}，y′＞0
x∈{
，+∞}，y′＜0，所以，当x=
时，y极大=
，无极小值
②当n≥2时，y′=-n（1-x）n•x2n-1+（2n-1）x（2n-2）．（1-x）n=x2n-1．（1-x）n[（2n-1）-（3n-1）x]
令y′=0则x1=0，x2=
，x3=1且x1＜x2＜x3
①当n为正偶数时，随x的变化，y′和y的变化如下：
点评：该题考查函数的求导公式，和数学归纳法的使用，注意画图，有点难度
（2）利用导数公式求函数的导数，画图求函数的单调性，根据导数求极值，
（3）利用导数求导和利用数学归纳法，在当a=1时和当a≥2时的条件下证明
解答：解：（1）f′2（x）=2x，∴2[x1+
（x2-x1）]=（x22-x12）/（x2-x1）∴x2+x1=2x1+
（x2-x1）⇒λ=2（2）令y=F（X）=f′2n-1（x）•fn（1-x）=（1-x）n•x2n-1，则
①当n=1时，y=x-x2，y′=1-2x，令y′=o，得x=
，x∈{-∞，}，y′＞0x∈{
，+∞}，y′＜0，所以，当x=时，y极大=，无极小值②当n≥2时，y′=-n（1-x）n•x2n-1+（2n-1）x（2n-2）．（1-x）n=x2n-1．（1-x）n[（2n-1）-（3n-1）x]
令y′=0则x1=0，x2=
，x3=1且x1＜x2＜x3①当n为正偶数时，随x的变化，y′和y的变化如下：
点评：该题考查函数的求导公式，和数学归纳法的使用，注意画图，有点难度
练习册系列答案
名题金卷系列答案
相关题目