题目内容

对数列，如果及，使成立，其中，则称为阶递归数列．给出下列三个结论：

①        若是等比数列，则为阶递归数列；

②        若是等差数列，则为阶递归数列；

③        若数列的通项公式为，则为阶递归数列．

其中正确结论的个数是（   ）

A．0              B．1             C．2             D．3

 

【答案】

D

【解析】对于①,令k=1得，,又 是等比数列，所以存在，①正确。

对于②，令k=2得，因为是等差数列，所以，故存在，②正确。

对于③，令k=3得，

因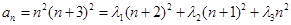为，所以

，

,所以③正确

 

练习册系列答案
相关题目
已知定义在R上的奇函数f(x)=
-2x+b
2x+1+a
．
（1）求a、b的值；
（2）若不等式-m2+(k+2)m-
3
2
＜f(x)＜m2+2km+k+
5
2
对一切实数x及m恒成立，求实数k的取值范围；
（3）若函数g（x）是定义在R上的周期为2的奇函数，且当x∈（-1，1）时，g（x）=f（x）-x，求方程g（x）=0的所有解．
（A类）定义在R上的函数y=f（x），对任意的a，b∈R，满足f（a+b）=f（a）•f（b），当x＞0时，有f（x）＞1，其中f（1）=2
（1）求f（0）、f（-1）的值；  （2）证明y=f（x）在（0，+∞）上是增函数；（3）求不等式f（x+1）＜4的解集．
（B类）已知定义在R上的奇函数f(x)= 
-2x+b
2x+1+a
．
（1）求a，b的值；
（2）若不等式-m2+(k+2)m-
3
2
＜f(x)＜m2+2km+k+
5
2
对一切实数x及m恒成立，求实数k的取值范围；
（3）定义：若存在一个非零常数T，使得f（x+T）=f（x）对定义域中的任何实数x都恒成立，那么，我们把f（x）叫以T为周期的周期函数，它特别有性质：对定义域中的任意x，f（x+nT）=f（x），（n∈Z）．若函数g（x0是定义在R上的周期为2的奇函数，且当x∈（-1，1）时，g（x）=f（x）-x，求方程g（x）=0的所有解．
已知定义在R上的奇函数．
（1）求a、b的值；
（2）若不等式对一切实数x及m恒成立，求实数k的取值范围；
（3）若函数g（x）是定义在R上的周期为2的奇函数，且当x∈（-1，1）时，g（x）=f（x）-x，求方程g（x）=0的所有解．

已知函数对且恒有，则使成立的实数的取值范围是___▲___.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网