题目内容
已知定义域为R的函数f（x）为奇函数，且满足f（x+2）=-f（x），当x∈[0，1]时，f（x）=2x-1，则
= ．
【答案】分析：由题意可得f（x）的周期为4，而由对数的运算可化为f（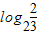
），再结合奇函数的性质可化为-f（
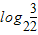），而
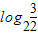∈[0，1]，代入已知公式可得答案．
解答：解：由题意可得：f（x+4）=f[（x+2）+2]=-f（x+2）=f（x），故f（x）的周期为4
故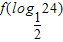
=f（-log224）=f（-log2（8×3））=f（-3-log23）=f（4-3-log23）
=f（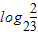
）=-f（-
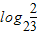）=-f（
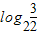），而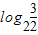
∈[0，1]
故-f（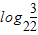
）=
=
=-
，
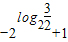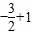故答案为：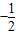
点评：本题考查函数的性质，正确推理并运用函数的性质是解决问题的关键，属基础题．
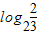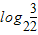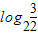），再结合奇函数的性质可化为-f（），而∈[0，1]，代入已知公式可得答案．解答：解：由题意可得：f（x+4）=f[（x+2）+2]=-f（x+2）=f（x），故f（x）的周期为4
故
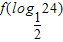=f（-log224）=f（-log2（8×3））=f（-3-log23）=f（4-3-log23）=f（
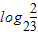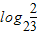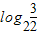）=-f（-）=-f（），而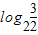∈[0，1]故-f（
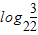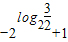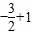）===-，故答案为：
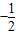
点评：本题考查函数的性质，正确推理并运用函数的性质是解决问题的关键，属基础题．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目