题目内容
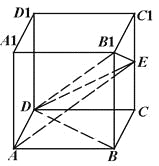
【题目】在棱长为2的正方体![]() 中,设
中,设![]() 是棱
是棱![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
试题本题考查了空间中的垂直与平行的判断与性质的应用问题,也考查了求几何体的体积的问题,(1)通过证明![]() 平面
平面![]() ,得出
,得出![]() ;(2)通过
;(2)通过![]() 的中位线证明线线平行,再证明线面平行;(3)点
的中位线证明线线平行,再证明线面平行;(3)点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,利用等积法求出三棱锥
的距离,利用等积法求出三棱锥![]() 的体积.
的体积.
试题解析:解:(1)【证明】连接BD,AE.因四边形ABCD为正方形,故![]() ,
,
因![]() 底面ABCD,
底面ABCD,![]() 面ABCD,故
面ABCD,故![]() ,又
,又![]() ,
,
故![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() .
.
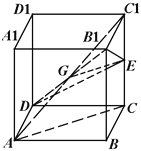
(2)连接![]() ,设
,设![]() ,连接
,连接![]() ,
,
则![]() 为
为![]() 中点,而
中点,而![]() 为
为![]() 的中点,故
的中点,故![]() 为三角形
为三角形![]() 的中位线,
的中位线,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
(3)由(2)知,点A到平面![]() 的距离等于C到平面
的距离等于C到平面![]() 的距离,
的距离,
故三棱锥![]() 的体积
的体积![]() ,
,
而![]() ,
,
三棱锥![]() 的体积为
的体积为![]() .…12分.
.…12分.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产一件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元;假设甲机床某天生产50件零件,请估计甲机床该天的日利润(单位:元);
(3)从甲、乙机床生产的零件指标在[90,95)内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
