题目内容
设函数
是定义在R上的奇函数，且函数
的图象在
处的切线方程为
．
（Ⅰ）求
的值；
（Ⅱ）若对任意
都有
成立，求实数
的取值范围；
都有
成立，求实数
的取值范围．
解析：（Ⅰ）∵ 函数
是定义在R上的奇函数，∴ 
∵ 
∴ 
．
又
在
处的切线方程为
，由
∴ 
，且
， ∴ 
得
（Ⅱ）
依题意
对任意
恒成立，
∴ 
对任意恒成立，
即 
对任意恒成立，∴ 
．
（Ⅲ）解一：
，
即
∴ 
即
对任意
恒成立，
记
，其中
则 
∴ 当
时，
，
在
上单调递增，
当
时，
，在
上单调递减，
∴ 在
上的最大值是
，则
；
记
，其中
则 
所以 
在
上单调递减，
∴ 即在上的最小值是
，则
；
的取值范围是
． 
练习册系列答案
小学教材全测系列答案
相关题目
是定义在R上的奇函数，对任意实数
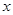有
成立．
是周期函数，并指出其周期；
，求
的值；
，且
是偶函数，求实数
的值．
是定义在R上的函数，其中
的导函数为
，满足
对于
恒成立，则（
）
B.
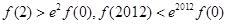
D.
是定义在R上的奇函数，且当x
0时，
是等差数列，且a3<0，则
的值为： 
是定义在R上的偶函数，且对任意的
恒有
，
时，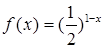
，则其中所有正确命题的序号是_____________.
上是减函数，在
上是增函数；
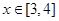时，
. 
是定义在R上的奇函数，若
， 
的取值范围是( )
B．
D．