Question

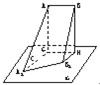
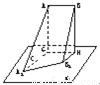
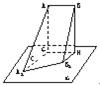线段AB与平面α平行，α的斜线A₁A、B₁B与α所成的角分别为30°和60°，且∠A₁AB=∠B₁BA=90°，AB=6，A₁B₁=10，求AB与平面α的距离．

Answer 1

分析：求直线到平面的距离常转化为求点到平面的距离．作AG⊥α于点G，BH⊥α于点H，连接A₁G、B₁H、GH，作B₁C⊥A₁G于点C，则通过解三角形可得AG的长度．另外，此题还要考虑到当A₁、B₁分居平面AH两侧时，AG的长度．故本题AB与平面α的距离有两个答案．

解答：解：如图，作AG⊥α于点G，BH⊥α于点H，连接A₁G、B₁H、GH，
∵A₁A⊥AB，
∴A₁G⊥GH．
同理，B₁H⊥GH．
作B₁C⊥A₁G于点C，则B₁C=GH=AB=6，∠AA₁G=30°，∠BB₁H=60°．
设B₁H=x，则CG=B₁H=x，AG=BH=

3

x，A₁G=3x=x+A₁C=x+8．
所以x=4，AG=BH=4

3

．
当A₁、B₁分居平面AH两侧时，类似可得AG=BH=2

3

．
故求AB与平面α的距离为4

3

或2

3

．

点评：本小题主要考查直线到平面的距离、点到平面的距离、直线与平面所成的角等基本知识，同时考查空间想象能力和推理、运算能力．