题目内容
如图2-26,已知⊙O和⊙O′外切于点E,AC是外公切线,A、C是切点,AB是⊙O的直径,BD是⊙O′的切线,D是切点,求证:AB=BD.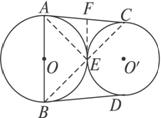
图2-26
证明:作两圆内公切线EF,连结AE、BE、CE.
∵∠FAE=∠FEA,∠FEC=∠FCE,
∴∠AEF+∠FEC=90°,即∠AEC=90°.
∵AB是直径,∴∠AEB=90°.
∴B、E、C在一条直线上.
∵AC切⊙O于A,∴AB⊥AC.
在Rt△ABC中,由射影定理,得AB2=BE·BC.
又BD切⊙O′于D,由切割线定理BD2=BE·BC,
∴AB2=BD2.∴AB=BD.
练习册系列答案
相关题目
11、某校为了了解学生的身体素质情况，对初三（2）班的50名学生进行了立定跳远、铅球、100米三个项目的测试，每个项目满分为10分．如图，是将该学生所得的三项成绩（成绩均为整数）之和进行整理后，分成5组画出的频率分布直方图，已知从左至右前4个小组的频率分别为0.02，0.1，0.12，0.46．
已知某单位有40名职工，现要从中抽取5名职工，将全体职工随机按l～40编号，并按编号顺序平均分成5组，按系统抽样方法在各组内抽取一个号码．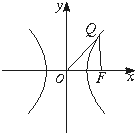
已知△OFQ的面积为2