题目内容
设函数f(x)=ax3-(a+b)x2+bx+c,其中a>0,b,c∈R.
(1)若 =0,求函数f(x)的单调增区间;
=0,求函数f(x)的单调增区间;
(2)求证:当0≤x≤1时,|f'(x)|≤max{f'(0),f'(1)}.(注:max{a,b}表示a,b中的最大值)
解:(1)′由 =0,得a=b. …(1分)
=0,得a=b. …(1分)
故f(x)=ax3-2ax2+ax+c.
由f′(x)=a(3x2-4x+1)=0,得x1= ,x2=1.…(2分)列表:
,x2=1.…(2分)列表:
由表可得,函数f(x)的单调增区间是(-∞, )及(1,+∞).…(4分)
)及(1,+∞).…(4分)
(2)f′(x)=3ax2-2(a+b)x+b=3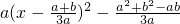 .
.
①当 时,则f′(x)在[0,1]上是单调函数,
时,则f′(x)在[0,1]上是单调函数,
所以f′(1)≤f′(x)≤f′(0),或f′(0)≤f′(x)≤f′(1),且f′(0)+f′(1)=a>0.
所以|f′(x)|≤max{f′(0),f′(1)}.…(8分)
②当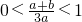 ,即-a<b<2a,则
,即-a<b<2a,则 ≤f′(x)≤max{f′(0),f′(1)}.
≤f′(x)≤max{f′(0),f′(1)}.
(i) 当-a<b≤ 时,则0<a+b≤
时,则0<a+b≤ .
.
所以 f′(1) =
=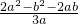 =
=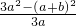 ≥
≥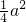 >0.
>0.
所以|f′(x)|≤max{f′(0),f′(1)}. …(12分)
(ii) 当 <b<2a时,则
<b<2a时,则 <0,即a2+b2-
<0,即a2+b2-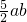 <0.
<0.
所以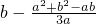 =
=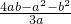 >
>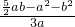 >0,即f′(0)>
>0,即f′(0)> .
.
所以|f′(x)|≤max{f′(0),f′(1)}.
综上所述:当0≤x≤1时,|f′(x)|≤max{f′(0),f′(1)}.…(16分)
分析:(1)由 =0,可得a=b,所以f(x)=ax3-2ax2+ax+c.由f'(x)=a(3x2-4x+1)=0,得x1=
=0,可得a=b,所以f(x)=ax3-2ax2+ax+c.由f'(x)=a(3x2-4x+1)=0,得x1= ,x2=1,利用导数大于0,可得函数f(x)的单调增区间;
,x2=1,利用导数大于0,可得函数f(x)的单调增区间;
(2)先求导函数f'(x)=3ax2-2(a+b)x+b=3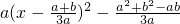 .由于函数的对称轴为
.由于函数的对称轴为 ,
,
0≤x≤1,故需要进行分类讨论:①当 时,则f'(x)在[0,1]上是单调函数;②当
时,则f'(x)在[0,1]上是单调函数;②当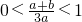 ,即-a<b<2a,则
,即-a<b<2a,则 ≤f'(x)≤max{f'(0),f'(1)},从而可证得结论.
≤f'(x)≤max{f'(0),f'(1)},从而可证得结论.
点评:本题以函数为载体,主要考查用导数法研究函数的单调性,基本思路是:当函数为增函数时,导数大于零;当函数为减函数时,导数小于零,考查二次函数的最值,解题的关键是分类讨论.
 =0,得a=b. …(1分)
=0,得a=b. …(1分)故f(x)=ax3-2ax2+ax+c.
由f′(x)=a(3x2-4x+1)=0,得x1=
 ,x2=1.…(2分)列表:
,x2=1.…(2分)列表:| x | (-∞, ) ) |  | ( ,1) ,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
 )及(1,+∞).…(4分)
)及(1,+∞).…(4分)(2)f′(x)=3ax2-2(a+b)x+b=3
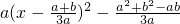 .
.①当
 时,则f′(x)在[0,1]上是单调函数,
时,则f′(x)在[0,1]上是单调函数,所以f′(1)≤f′(x)≤f′(0),或f′(0)≤f′(x)≤f′(1),且f′(0)+f′(1)=a>0.
所以|f′(x)|≤max{f′(0),f′(1)}.…(8分)
②当
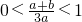 ,即-a<b<2a,则
,即-a<b<2a,则 ≤f′(x)≤max{f′(0),f′(1)}.
≤f′(x)≤max{f′(0),f′(1)}.(i) 当-a<b≤
 时,则0<a+b≤
时,则0<a+b≤ .
.所以 f′(1)
 =
=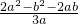 =
=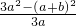 ≥
≥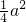 >0.
>0.所以|f′(x)|≤max{f′(0),f′(1)}. …(12分)
(ii) 当
 <b<2a时,则
<b<2a时,则 <0,即a2+b2-
<0,即a2+b2-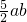 <0.
<0.所以
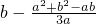 =
=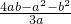 >
>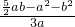 >0,即f′(0)>
>0,即f′(0)> .
.所以|f′(x)|≤max{f′(0),f′(1)}.
综上所述:当0≤x≤1时,|f′(x)|≤max{f′(0),f′(1)}.…(16分)
分析:(1)由
 =0,可得a=b,所以f(x)=ax3-2ax2+ax+c.由f'(x)=a(3x2-4x+1)=0,得x1=
=0,可得a=b,所以f(x)=ax3-2ax2+ax+c.由f'(x)=a(3x2-4x+1)=0,得x1= ,x2=1,利用导数大于0,可得函数f(x)的单调增区间;
,x2=1,利用导数大于0,可得函数f(x)的单调增区间;(2)先求导函数f'(x)=3ax2-2(a+b)x+b=3
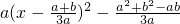 .由于函数的对称轴为
.由于函数的对称轴为 ,
,0≤x≤1,故需要进行分类讨论:①当
 时,则f'(x)在[0,1]上是单调函数;②当
时,则f'(x)在[0,1]上是单调函数;②当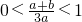 ,即-a<b<2a,则
,即-a<b<2a,则 ≤f'(x)≤max{f'(0),f'(1)},从而可证得结论.
≤f'(x)≤max{f'(0),f'(1)},从而可证得结论.点评:本题以函数为载体,主要考查用导数法研究函数的单调性,基本思路是:当函数为增函数时,导数大于零;当函数为减函数时,导数小于零,考查二次函数的最值,解题的关键是分类讨论.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |