题目内容

已知棱长为2的正方体的八个顶点都在同一个球面上，求这个球的体积

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
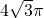
D.
24π

C
分析：根据已知中棱长为2的正方体的八个顶点都在同一个球面上，我们可以计算出球的半径，代入球的体积公式，即可得到答案．
解答：若棱长为2的正方体的八个顶点都在同一个球面上，
则球的直径等于正方体的对角线长
即2R=2 $\text{[math]}$
∴R= $\text{[math]}$
则球的体积V= $\text{[math]}$ = $\text{[math]}$
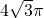
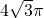
故选C
点评：本题考查的知识点是球的体积及球内接多面体，其中根据球内接正方体的棱长求出球的半径是解答本题的关键．

练习册系列答案

教学大典系列答案

学考A加卷中考考点优化分类系列答案

发散思维新课堂系列答案

明日之星课时优化作业系列答案

同步首选全练全测系列答案

学效评估同步练习册系列答案

高中新课标同步用书全优课堂系列答案

实验探究报告册系列答案

金版学案高中同步辅导与检测系列答案

名师金典高中新课标同步攻略与测评系列答案

相关题目

已知棱长为2的正方体的八个顶点都在同一个球面上，求这个球的体积（　　）

已知棱长为2的正方体ABCD-A₁B₁C₁D₁中，M为AB的中点，P是平面ABCD内的动点，且满足条件PD₁=3PM，则动点P在平面ABCD内形成的轨迹是

已知棱长为2的正方体，内切球O，若在正方体内任取一点，则这一点不在球内的概率为

．
在区间（0，1）中随机地取出两个数，则两数之和小于

已知棱长为2的正方体，内切球O，若在正方体内任取一点，则这一点不在球内的概率为

已知棱长为2的正方体的八个顶点都在同一个球面上，若在球内任取一点，则这一点q恰在正方体内的概率为（　　）