题目内容
已知函数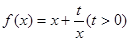 和点
和点 ,过点
,过点 作曲线
作曲线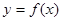 的两条切线
的两条切线 、
、 ,切点分别为
,切点分别为 、
、 .
.
(Ⅰ)设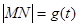 ,试求函数
,试求函数 的表达式;
的表达式;
(Ⅱ)是否存在 ,使得
,使得 、
、 与
与 三点共线.若存在,求出
三点共线.若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数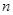 ,在区间
,在区间 内总存在
内总存在 个实数
个实数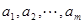 ,
, ,使得不等式
,使得不等式 成立,求
成立,求 的最大值.
的最大值.
(Ⅰ)函数 的表达式为
的表达式为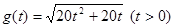 .
.
(Ⅱ)存在 ,使得点
,使得点 、
、 与
与 三点共线,且
三点共线,且 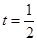 .
.
(Ⅲ) 的最大值为
的最大值为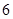 .
.
解析试题分析:(Ⅰ)设 、
、 两点的横坐标分别为
两点的横坐标分别为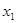 、
、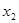 ,
, 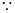
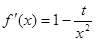 ,
,
∴切线 的方程为:
的方程为: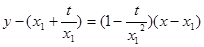 ,
,
又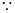 切线
切线 过点
过点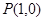 ,
, 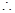 有
有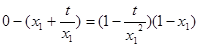 ,即
,即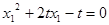 , (1)
, (1)
同理,由切线 也过点
也过点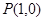 ,得
,得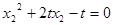 .(2)
.(2)
由(1)、(2),可得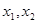 是方程
是方程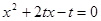 的两根,
的两根,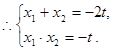 ( * )
( * )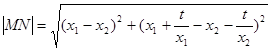
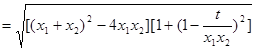 ,
,
把( * )式代入,得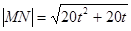 ,
,
因此,函数 的表达式为
的表达式为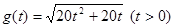 .
.
(Ⅱ)当点 、
、 与
与 共线时,
共线时,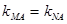 ,
,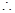
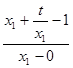 =
=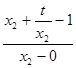 ,即
,即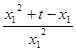 =
=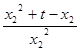 ,
,
化简,得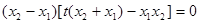 ,
,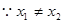 ,
,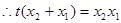 . (3)
. (3)
把(*)式代入(3),解得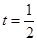 .
. 存在
存在 ,使得点
,使得点 、
、 与
与 三点共线,且
三点共线,且 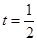 .
.
(Ⅲ)解法 :易知
:易知 在区间
在区间 上为增函数,
上为增函数,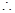
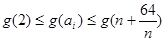
 ,
,
则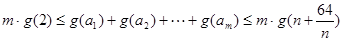 .
.
依题意,不等式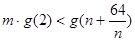 对一切的正整数
对一切的正整数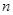 恒成立,
恒成立,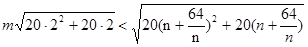 ,
,
即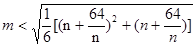 对一切的正整数
对一切的正整数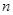 恒成立.
恒成立.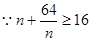 ,
, 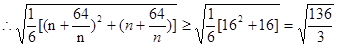 ,
,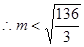 .
.
由于 为正整数,
为正整数,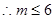 .
.
又当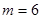 时,存在
时,存在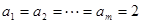 ,
,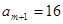 ,对所有的
,对所有的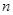 满足条件.
满足条件.
因此, 的最大值为
的最大值为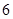 .
.
解法 :依题意,当区间
:依题意,当区间 的长度最小时,
的长度最小时,
得到的 最大值,即是所求值.
最大值,即是所求值.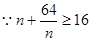 ,
,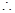 长度最小的区间为
长度最小的区间为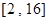
当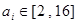
 时,与解法
时,与解法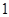

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
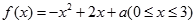 的最大值为
的最大值为 ,最小值为
,最小值为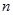 ,其中
,其中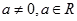 .
.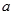 表示);
表示);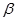 的顶点与平面直角坐标系
的顶点与平面直角坐标系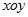 中的原点
中的原点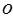 重合,始边与
重合,始边与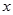 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点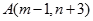 .求
.求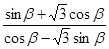 的值.
的值.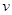 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度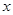 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当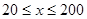 时,车流速度
时,车流速度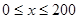 时,求函数
时,求函数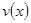 的表达式;
的表达式;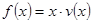 可以达到最大,并求出最大值.(精确到1辆/小时).
可以达到最大,并求出最大值.(精确到1辆/小时).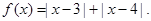
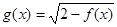 的定义域;
的定义域;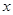 满足
满足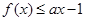 ,试求实数
,试求实数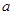 的取值范围.
的取值范围.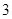 年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第
年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第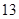 个月开始,每月工资比前一个月增加
个月开始,每月工资比前一个月增加 直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多
直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多 元.
元. 个月还清贷款(
个月还清贷款( ),试用
),试用 表示小王第
表示小王第 )个月的还款额
)个月的还款额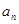 ;
; 时,小王将在第几个月还清最后一笔贷款?
时,小王将在第几个月还清最后一笔贷款? 元的基本生活费?(参考数据:
元的基本生活费?(参考数据: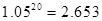 )
)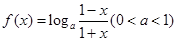 .
. 的定义域
的定义域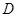 ,并判断
,并判断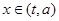 时,函数
时,函数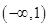 ,求
,求 与
与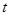 的值.
的值.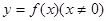 对于任意的
对于任意的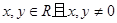 满足
满足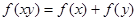 .
.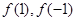 的值;
的值; 为偶函数;
为偶函数;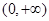 上是增函数,解不等式
上是增函数,解不等式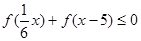
 ,都有f(x)-2mx≤1成立,求实数m的取值范围.
,都有f(x)-2mx≤1成立,求实数m的取值范围.