题目内容
已知函数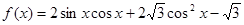 ,
, .
.
(1)求函数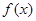 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)在锐角三角形 中,若
中,若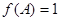 ,
,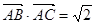 ,求△
,求△ 的面积.
的面积.
【答案】
(1)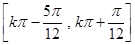 (
(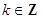 );(2)
);(2)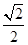 .
.
【解析】
试题分析:(1)三角函数问题一般都是要把三角函数化为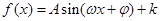 形式,然后利用正弦函数的知识解决问题,本题中选用二倍角公式和降幂公式化简为
形式,然后利用正弦函数的知识解决问题,本题中选用二倍角公式和降幂公式化简为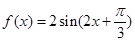 ;(2)三角形的面积公式很多,具体地要选用哪个公式,要根据题意来确定,本题中已知
;(2)三角形的面积公式很多,具体地要选用哪个公式,要根据题意来确定,本题中已知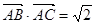 ,而
,而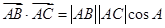 ,因此我们选面积公式
,因此我们选面积公式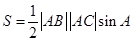 ,正好由已知条件可求出
,正好由已知条件可求出 ,也即求出
,也即求出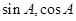 ,从而得面积.
,从而得面积.
试题解析:(1)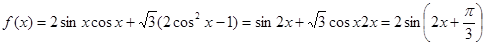 , (2分)
, (2分)
所以,函数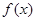 的最小正周期为
的最小正周期为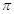 .
(1分)
.
(1分)
由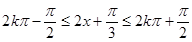 (
( ),
(2分)
),
(2分)
得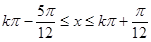 (
(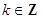 ),
(2分)
),
(2分)
所以,函数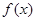 的单调递增区间是
的单调递增区间是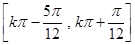 (
(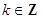 ). (1分)
). (1分)
(2)由已知,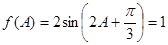 ,所以
,所以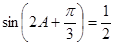 , (1分)
, (1分)
因为 ,所以
,所以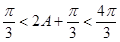 ,所以
,所以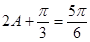 ,从而
,从而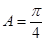 . (2分)
. (2分)
又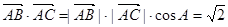 ,,所以,
,,所以,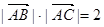 , (1分)
, (1分)
所以,△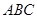 的面积
的面积 . (2分)
. (2分)
考点:(1)三角函数的性质;(2)三角形的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目