Question

如图，四面体PABC中，PA、PB、PC两两垂直，PA=PB=2，PC=4，E是AB的中点，F是CE的中点.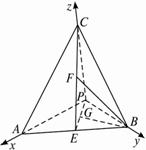

(1)写出点B、C、E、F的坐标；

(2)求BF与底面ABP所成的角的余弦值.

Answer 1

解析：(1)如图，以PA为x轴，PB为y轴，PC为z轴，P为原点建立空间直角坐标系，则B点坐标为(0,2,0)，C点坐标为(0,0,4),A点坐标为(2,0,0).

∵E为AB中点，

∴E(1,1,0).

∵F为中点，

∴F(,,2).

(2)设G为PE中点，则G(,,0).

∵PA、PB、PC两两互相垂直，

∴PC⊥面ABP.

∵F、G分别为CE、PE中点，

∴FG∥PC.

∴FG⊥面ABP.

故∠FBG为BF与面ABP所成的角.

∴∠FBG=〈,〉,=(,-,2),=(,-,0).?

∴cos〈,〉= = =.