题目内容

抛物线y2=2px(p＞0)的内接正三角形OAB,其中一个顶点O在坐标原点,求这个正三角形外接圆的方程.

解:依题意可知圆心在x轴上,且过原点.故可设所求的圆的方程为x2+y2+Dx=0,

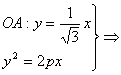A(6p,2p),代入圆的方程得36p2+12p2+D·6p=0,∴D=-8p.

∴所求的圆的方程为x2+y2-8px=0.

练习册系列答案
相关题目
精英家教网如图过抛物线y2=2px（p＞0）的焦点F的直线依次交抛物线及准线于点A，B，C，若|BC|=2|BF|，且|AF|=3，则抛物线的方程为（　　）
A、y2=
3
2
x
B、y2=9x
C、y2=
9
2
x
D、y2=3x
抛物线y2=2px（p＞0）上的点M（4，y）到焦点F的距离为5，O为坐标原点，则△OFM的面积为
2
2
．
抛物线y2=2px，（p＞0）绕焦点依逆时针方向旋转90°所得抛物线方程为…（　　）
（2012•泉州模拟）若抛物线y2=2px（p＞0）的焦点到双曲线x2-y2=1的渐近线的距离为
3
2
2
，则p的值为（　　）
过点A（-1，0）作抛物线y2=2px（p＞0）的两条切线，切点分别为B、C，且△ABC是正三角形，则抛物线方程为
y2=
4
3
x
y2=
4
3
x
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网