题目内容
在a>0,b>0的条件下,三个结论:
①
≤
,
②
≤
,
③
+
≥a+b,
其中正确的个数是( )
①
| 2ab |
| a+b |
| a+b |
| 2 |
②
| a+b |
| 2 |
|
③
| b2 |
| a |
| a2 |
| b |
其中正确的个数是( )
分析:用作差比较法证明①②③都正确,从而得到结论.
解答:解:在a>0,b>0的条件下,
由
-
=
=
=
≥0,可得①正确.
由
-(
)2=
=
≥0,可得
≥(
)2,
故有
≥
,故②正确.
由
+
-(a+b)=
+
=(b-a)(
-
)=(b-a)(
-
),
当b>a>0时,(b-a)>0,
>
,(
-
)>0,(b-a)(
-
)>0.
当a>b>0时,(b-a)<0,
<
,(
-
)<0,(b-a)(
-
)>0.
当a=b 时,显然(b-a)(
-
)=0.
综上,(b-a)(
-
)≥0,故有
+
≥a+b,故③正确.
故选D.
由
| a+b |
| 2 |
| 2ab |
| a+b |
| (a+b)2- 4ab |
| 2(a+b) |
| a2+b2- 2ab |
| 2(a+b) |
| (a-b)2 |
| 2(a+b) |
由
| a2+b2 |
| 2 |
| a+b |
| 2 |
| 2a2+2b2-a2-b2-2ab |
| 4 |
| (a-b)2 |
| 4 |
| a2+b2 |
| 2 |
| a+b |
| 2 |
故有
|
| a+b |
| 2 |
由
| b2 |
| a |
| a2 |
| b |
| b2-a2 |
| a |
| a2-b2 |
| b |
| a+b |
| a |
| a+b |
| b |
| b |
| a |
| a |
| b |
当b>a>0时,(b-a)>0,
| b |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
当a>b>0时,(b-a)<0,
| b |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
当a=b 时,显然(b-a)(
| b |
| a |
| a |
| b |
综上,(b-a)(
| b |
| a |
| a |
| b |
| b2 |
| a |
| a2 |
| b |
故选D.
点评:本题主要考查基本不等式的应用,用比较法证明不等式,体现了分类讨论的数学思想,式子的变形是解题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
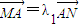 ,
,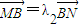 ,问λ1+λ2是否为定值?说明理由.
,问λ1+λ2是否为定值?说明理由.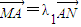 ,
,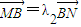 ,问λ1+λ2是否为定值?说明理由.
,问λ1+λ2是否为定值?说明理由.