题目内容
已知函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0<φ<| π |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
(1)求f(x)的解析式;
(2)求|f(x)+1|+
| π |
| 2 |
分析:通过函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0<φ<
)的图象与x轴的交点中,相邻两个交点之间的距离为
,求出函数的周期,确定ω的值,利用图象上一个最低点位M(
,-2).求出A,结合0<φ<
,求出φ的值,即可得到函数的解析式.
| π |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
| π |
| 2 |
解答:解:函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0<φ<
)的图象与x轴的交点中,相邻两个交点之间的距离为
,所以函数的周期为:π,所以ω=
=2;
图象上一个最低点位M(
,-2),所以A=2,并且-2=2sin(2×
+φ),因为0<φ<
,所以φ=
,
(1)函数的解析式为:f(x)=2sin(2x+
);
(2)函数|f(x)+1|+
的单调区间就是|f(x)+1|的单调区间,|f(x)+1|=|2sin(2x+
)+1|,令g(x)=|2sin(2x+
)+1|,作出g(x)的图象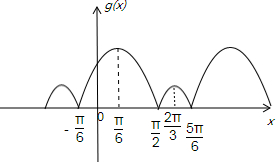
所以|f(x)+1|+
的单调区间的单调增区间为:[kπ-
,kπ+
],[kπ+
,kπ+
],k∈Z;
单调减区间为:[kπ+
,kπ+
],[kπ+
,kπ+
],k∈Z
| π |
| 2 |
| π |
| 2 |
| 2π |
| T |
图象上一个最低点位M(
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 2 |
| π |
| 6 |
(1)函数的解析式为:f(x)=2sin(2x+
| π |
| 6 |
(2)函数|f(x)+1|+
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |

所以|f(x)+1|+
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| 2π |
| 3 |
单调减区间为:[kπ+
| π |
| 6 |
| π |
| 2 |
| 2π |
| 3 |
| 5π |
| 6 |
点评:本题是中档题,考查三角函数的解析式的求法,函数单调性的求法,利用函数的图象解决函数的单调性,方便简洁,注意转化思想的应用,考查计算能力.

练习册系列答案
相关题目