题目内容
 如图所示,四棱锥P-ABCD的底面ABCD为菱形,且∠DAB=60°,AB=2,E为PC的中点,DE=
如图所示,四棱锥P-ABCD的底面ABCD为菱形,且∠DAB=60°,AB=2,E为PC的中点,DE=| 2 |
(1)求证:PA⊥平面ABCD;
(2)求二面角E-PD-B的平面角的大小.
分析:(1)先证明OE⊥平面ABCD,再利用OE∥PA,可得PA⊥平面ABCD;
(2)建立空间直角坐标系,求出平面PDE,平面PBD的一个法向量,利用向量的夹角公式,即可求得结论.
(2)建立空间直角坐标系,求出平面PDE,平面PBD的一个法向量,利用向量的夹角公式,即可求得结论.
解答:(1)证明:连接AC,BD,相交于O,连接OE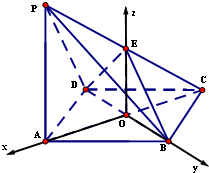
设点D到面PAC的距离为h,则直线DE与平面PAC所成角的正弦值为sin45°=
=
,∴h=1
∵底面ABCD为菱形,且∠DAB=60°,AB=2,∴DO=1
∴DO⊥平面PAC
∴DO⊥OE,且OE=
=1
∵CO=
AC=
,∴OE2+OC2=CE2
∴OC⊥OE
∵OC∩DO=O,∴OE⊥平面ABCD
∵OE∥PA,∴PA⊥平面ABCD;
(2)解:建立如图所示的空间直角坐标系,则O(0,0,0),A(
,0,0),B(0,1,0),C(-
,0,0),D(0,-1,0),P(
,0,2),E(0,0,1)
设平面PDE的一个法向量为
=(x,y,z),则
,∴
∴取
=(
,3,-3)
设平面PBD的一个法向量为
=(x′,y′,z′),则
,∴
∴取
=(2
,0,-3)
∴cos<
,
>=
=
∴求二面角E-PD-B的平面角的大小为arccos
.

设点D到面PAC的距离为h,则直线DE与平面PAC所成角的正弦值为sin45°=
| h |
| DE |
| h | ||
|
∵底面ABCD为菱形,且∠DAB=60°,AB=2,∴DO=1
∴DO⊥平面PAC
∴DO⊥OE,且OE=
| DE2-DO2 |
∵CO=
| 1 |
| 2 |
| 3 |
∴OC⊥OE
∵OC∩DO=O,∴OE⊥平面ABCD
∵OE∥PA,∴PA⊥平面ABCD;
(2)解:建立如图所示的空间直角坐标系,则O(0,0,0),A(
| 3 |
| 3 |
| 3 |
设平面PDE的一个法向量为
| n |
|
|
∴取
| n |
| 3 |
设平面PBD的一个法向量为
| m |
|
|
∴取
| m |
| 3 |
∴cos<
| n |
| m |
| ||||
|
|
| 5 |
| 7 |
∴求二面角E-PD-B的平面角的大小为arccos
| 5 |
| 7 |
点评:本题考查线面垂直,考查面面角,考查学生的计算能力,考查利用向量的方法,夹角空间角问题,求得平面的法向量是关键,

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.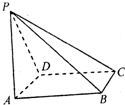 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,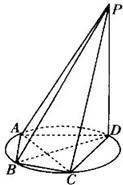 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.