题目内容
已知函数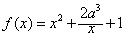 ,其中a>0,
,其中a>0,
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线y=1平行,求a的值;
(2)求函数f(x)在区间[1,2]上的最小值.
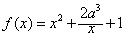 ,其中a>0,
,其中a>0,(1)若曲线y=f(x)在点(1,f(1))处的切线与直线y=1平行,求a的值;
(2)求函数f(x)在区间[1,2]上的最小值.
解: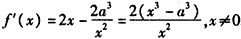 ,
,
(1)由题意可得f′(1)=2(1-a3)=0,解得a=1,
此时f(1)=4,在点(1,f(1))处的切线为y=4,与直线y=1平行,
故所求的a值为1;
(2)由f′(x)=0可得x=a,a>0,
①当0<a≤1时,f′(x)>0在(1,2]上恒成立,
所以y=f(x)在[1,2]上递增,所以f(x)在[1,2]上的最小值为f(1)=2a3+2;
②当1<a<2时,
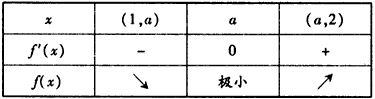
由上表可得y=f(x)在[1,2]上的最小值为f(a)=3a2+1;
③当a≥2时,f′(x)<0在[1,2)上恒成立,
所以y=f(x)在[1,2]上递减,所以f(x)在[1,2]上的最小值为f(2)=a3+5;
综上讨论,可知:
当0<a≤1时,y=f(x)在[1,2]上的最小值为f(1)=2a3+2;
当1<a<2时,y=f(x)在[1,2]上的最小值为f(a)=3a2+1;
当a≥2时,y=f(x)在[1,2]上的最小值为f(2)=a3+5。
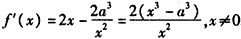 ,
,(1)由题意可得f′(1)=2(1-a3)=0,解得a=1,
此时f(1)=4,在点(1,f(1))处的切线为y=4,与直线y=1平行,
故所求的a值为1;
(2)由f′(x)=0可得x=a,a>0,
①当0<a≤1时,f′(x)>0在(1,2]上恒成立,
所以y=f(x)在[1,2]上递增,所以f(x)在[1,2]上的最小值为f(1)=2a3+2;
②当1<a<2时,

由上表可得y=f(x)在[1,2]上的最小值为f(a)=3a2+1;
③当a≥2时,f′(x)<0在[1,2)上恒成立,
所以y=f(x)在[1,2]上递减,所以f(x)在[1,2]上的最小值为f(2)=a3+5;
综上讨论,可知:
当0<a≤1时,y=f(x)在[1,2]上的最小值为f(1)=2a3+2;
当1<a<2时,y=f(x)在[1,2]上的最小值为f(a)=3a2+1;
当a≥2时,y=f(x)在[1,2]上的最小值为f(2)=a3+5。

练习册系列答案
相关题目
 ,其中a>0.
,其中a>0. ,其中a>0.
,其中a>0.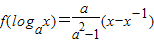 ,其中a>0且a≠1.
,其中a>0且a≠1.