题目内容

若A（x1，y1），B（x2，y2）是圆x2+y2=4上两点，且∠AOB=120°，则x1x2+y1y2=
 
．
分析：如图所示，建立直角坐标系．不妨取A（2，0），B（2cos120°，2sin120°），即可得出
OA
•
OB
．
解答：解：如图所示，建立直角坐标系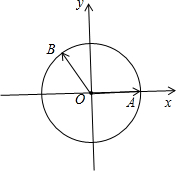．精英家教网
不妨取A（2，0），B（2cos120°，2sin120°），
即(-1，
3
)．
则
OA
•
OB
=-2+0=-2．
故答案为：-2．
点评：本题考查了直线与圆相交问题、数量积运算，属于基础题．
练习册系列答案
相关题目
给出下列命题：
①若
a
2+
b
2=0，则
a
=
b
=
0
；
②若A（x1，y1），B（x2，y2），则
1
2
AB
=(
x1+x2
2
，
y1+y2
2
)；
③已知
a
，
b
，
c
是三个非零向量，若
a
+
b
=
0
；，则|
a
•
c
|=|
b
•
c
|；
④已知λ1＞0，λ2＞0，
e1
，
e2
是一组基底，
a
=λ1
e1
+λ2
e2
，则
a
与
e1
不共线，
a
与
e2
也不共线；
⑤
a
与
b
共线?
a
•
b
=|
a
||
b
|．
其中正确命题的序号是
 
．
若
a
=（x1，y1），
b
=（x2，y2），且
a
∥
b
，则有（　　）
A、x1y2+x2y1=0
B、x1y2-x2y1=0，
C、x1x2+y1y2=0
D、x1x2-y1y2=0
若
a
=（x1，y1），
b
=（x2，y2），定义：
a
•
b
=x1x2+y1y2，已知
a
=（2cosx，1），
b
=（cosx，
3
sin2x），f（x）=
a
•
b
，x∈R
（1）若f(x)=1-
3
，且x∈[-
π
3
，
π
3
]，求x；
（2）若函数y=2sin2x的图象向左（或右）平移|m|(|m|＜
π
2
)个单位，再向上（或下）平移|n|个单位后得到函数y=f（x）的图象，求实数m，n的值．
定义空间两个向量的一种运算
a
⊕
b
=|
a
|-|
b
|sin＜
a
，
b
＞，则关于空间向量上述运算的以下结论中，
①
a
⊕
b
=
b
⊕
a
，
②λ（
a
⊕
b
）=（λ
a
）⊕
b
，
③（
a
⊕
b
）⊕
c
=（
a
⊕
c
）（
b
⊕
c
），
④若
a
=（x1，y1），
b
=（x2，y2），则
a
⊕
b
=|x1y2-x2y1|；
恒成立的个数有（　　）
若A（x1，y1），B（x2，y2），C（x3，y3）是函数f（x）图象上的任意三点，其中实数x1，x2，x3两两不等，实数y1，y2，y3两两不等．有以下命题：若x1，x2，x3是等差数列，则y1，y2，y3是等比数列．请写出一个满足上述命题的函数
y=2x等等
y=2x等等
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网