题目内容
20.经过坐标原点,且与圆(x-3)2+(y+1)2=2相切于第四象限的直线方程是( )| A. | x-y=0 | B. | x+y=0 | C. | x-7y=0 | D. | x+7y=0 |
分析 设所求直线方程为y=kx,即kx-y=0,利用圆心到直线的距离等于半径,结合切点在第四象限,即可得出结论.
解答 解:依题意,设所求直线方程为y=kx,即kx-y=0,
圆心到直线的距离为d=$\frac{|3k+1|}{\sqrt{{k}^{2}+1}}$=$\sqrt{2}$,解得k=-1或k=$\frac{1}{7}$(舍去),
∴所求直线方程是x+y=0.
故选:B.
点评 本题考查直线与圆相切时所满足的条件,灵活运用点到直线的距离公式化简求值,考查了数形结合的数学思想,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.如图,有一个几何体的三视图及其尺寸(单位:cm),则该几何体的表面积和体积分别为( )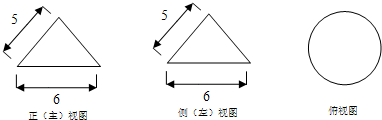

| A. | 24πcm2,12πcm3 | B. | 15πcm2,12πcm3 | C. | 24πcm2,36πcm3 | D. | 15πcm2,36πcm3 |
11.设函数f(x)=2+$\frac{2mx+sinx+mxcosx}{2+cosx}$,若f(x)在[-n,n]上的值域为[a,b],其中a,b,m,n∈R,且n>0,则a+b=( )
| A. | 0 | B. | 2 | C. | 4 | D. | 2m |
12.已知函数f(x)=$\left\{{\begin{array}{l}{{3^{-x}}-1,x≥0}\\{1-{3^x},x<0}\end{array}}$,则该函数是( )
| A. | 偶函数,且单调递增 | B. | 偶函数,且单调递减 | ||
| C. | 奇函数,且单调递增 | D. | 奇函数,且单调递减 |
20.下列四个命题中是假命题的是( )
| A. | 在△ABC中,角A,B所对边分别为a,b则sinA>sinB成立的充要条件是a>b | |||||||||
| B. | 若命题p:?x∈(0,+∞),sinx-x<0,命题q:?x0∈(0,+∞),e${\;}^{{x}_{0}}$<0,则p∧¬q为真命题 | |||||||||
| C. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一的实数λ,使$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |||||||||
| D. | 在一个2×2列联表中,由计算得k2=6.721,则有99%的把握确认这两个变量间有关系;可以参考独立性检验临界表
|