题目内容

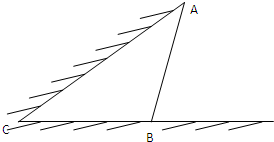如图所示，某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室．已知已有两面墙的夹角为60°（即∠C=60°），第三面围墙的长度为6米，即AB=6米，（两面墙的长均大于6米）．为了使得小老虎能健康成长，要求所建造的三角形露天活动室尽可能大．记∠ABC=θ，问当θ为多少时，所建造的三角形露天活动室的面积最大？
分析：先利用正弦定理，求得AC，BC的长，再利用三角形的面积公式，利用三角恒等变换公式化简，从而可求三角形面积的最大值．
解答：解：在△ABC中，
AC
sinθ
=
AB
sin
π
3
=
BC
sin(θ+
π
3
)

∴AC=4
3
sinθ，BC=4
3
sin(θ+
π
3
)
∴S△ABC=
1
2
AC•BC•sin
π
3
=12
3
sinθsin(θ+
π
3
)=6
3
(sin2θ+
3
sinθcosθ)
=6
3
[
1
2
+sin(2θ-
π
6
)]
∴2θ-
π
6
=
π
2
时，即θ=
π
3
时，面积最大为9
3

∴θ=
π
3
时，所建造的三角形露天活动室的面积最大
点评：本题重点考查正弦定理的运用，考查三角形的面积公式，考查三角恒等变换，构建三角函数模型是解题的关键．
练习册系列答案
相关题目
精英家教网如图所示，某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室，已知已有的两面墙的夹角为60°（即∠C=60°且两面墙的长度足够大），现有可供建造第三面围墙的材料6米（即AB长为6米），为了使得小老虎能健康成长，要求所建造的三角形露天活动室尽可能大，记∠ABC=θ．
（1）当θ=105°时，求所建造的三角形露天活动室的面积．
（2）问当θ为多少时，所建造的三角形露天活动室的面积最大？

如图所示，某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室，已知已有两面墙的夹角为（即），现有可供建造第三面围墙的材料米（两面墙的长均大于米），为了使得小老虎能健康成长，要求所建造的三角形露天活动室尽可能大，记，问当为多少时，所建造的三角形露天活动室的面积最大？

如图所示，某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室，已知已有两面墙的夹角为（即），现有可供建造第三面围墙的材料米（两面墙的长均大于米），为了使得小老虎能健康成长，要求所建造的三角形露天活动室尽可能大，记，问当为多少时，所建造的三角形露天活动室的面积最大？

                                                                         

如图所示，某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室，已知已有的两面墙的夹角为60°（即∠C=60°且两面墙的长度足够大），现有可供建造第三面围墙的材料6米（即AB长为6米），为了使得小老虎能健康成长，要求所建造的三角形露天活动室尽可能大，记∠ABC=θ．
（1）当θ=105°时，求所建造的三角形露天活动室的面积．
（2）问当θ为多少时，所建造的三角形露天活动室的面积最大？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网