题目内容
函数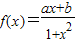 是定义在(-1,1)上的奇函数,且
是定义在(-1,1)上的奇函数,且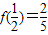
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)判断并证明f(x)在(-1,1)的单调性;
(Ⅲ)求满足f(t-1)+f(t)<0的t的范围.
【答案】分析:(Ⅰ)若奇函数在x=0处有定义,则f(0)=0,代入即可得b,再由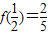 代入即可得a值;
代入即可得a值;
(Ⅱ)利用单调性定义即可证明;
(Ⅲ)利用函数的单调性和奇偶性将不等式中的f脱去,等价转化为关于t的不等式组,解之即可.
解答:解:(Ⅰ)∵函数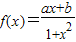 是定义在(-1,1)的奇函数
是定义在(-1,1)的奇函数
∴f(0)=0,∴b=0
∵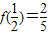 .
.
∴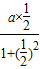 =
= ,∴a=1
,∴a=1
∴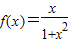 ;
;
(Ⅱ)函数f(x)在(-1,1)上为增函数,证明如下
在区间(-1,1)上任取x1,x2,令-1<x1<x2<1,
∴f(x1)-f(x2)=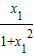 -
-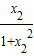 =
=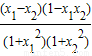 ;
;
∵-1<x1<x2<1
∴x1-x2<0,1-x1x2>0,1+x12>0,1+x22>0
∴f(x1)-f(x2)<0,即f(x1)<f(x2)
故函数f(x)在区间(-1,1)上是增函数;
(Ⅲ)∵f(t-1)+f(t)<0
∴f(t-1)<-f(t)
∴f(t-1)<f(-t)
∵函数f(x)在区间(-1,1)上是增函数
∴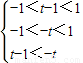
∴0<t< .
.
点评:本题考查函数奇偶性与单调性的性质应用,着重考查学生理解函数奇偶性与用定义证明单调性及解方程,解不等式组的能力,属于中档题.
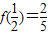 代入即可得a值;
代入即可得a值;(Ⅱ)利用单调性定义即可证明;
(Ⅲ)利用函数的单调性和奇偶性将不等式中的f脱去,等价转化为关于t的不等式组,解之即可.
解答:解:(Ⅰ)∵函数
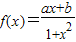 是定义在(-1,1)的奇函数
是定义在(-1,1)的奇函数∴f(0)=0,∴b=0
∵
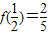 .
.∴
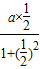 =
= ,∴a=1
,∴a=1∴
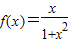 ;
;(Ⅱ)函数f(x)在(-1,1)上为增函数,证明如下
在区间(-1,1)上任取x1,x2,令-1<x1<x2<1,
∴f(x1)-f(x2)=
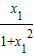 -
-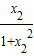 =
=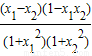 ;
;∵-1<x1<x2<1
∴x1-x2<0,1-x1x2>0,1+x12>0,1+x22>0
∴f(x1)-f(x2)<0,即f(x1)<f(x2)
故函数f(x)在区间(-1,1)上是增函数;
(Ⅲ)∵f(t-1)+f(t)<0
∴f(t-1)<-f(t)
∴f(t-1)<f(-t)
∵函数f(x)在区间(-1,1)上是增函数
∴
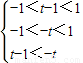
∴0<t<
 .
.点评:本题考查函数奇偶性与单调性的性质应用,着重考查学生理解函数奇偶性与用定义证明单调性及解方程,解不等式组的能力,属于中档题.

练习册系列答案
相关题目
 是定义在(-1,1)上的奇函数,且
是定义在(-1,1)上的奇函数,且 .
. 是定义在(–1,1)上的奇函数,且
是定义在(–1,1)上的奇函数,且 .
. 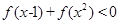
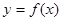 是定义在(1,4)上单调递减函数,且
是定义在(1,4)上单调递减函数,且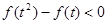 ,求
,求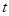 的取值范围。
的取值范围。 是定义在[2a+1,a+5]上的偶函数,则a的值为
是定义在[2a+1,a+5]上的偶函数,则a的值为 是定义在(–1,1)上的奇函数,且
是定义在(–1,1)上的奇函数,且 ,
,  .
.