题目内容
已知区域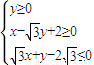 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率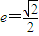 .
.(1)求圆C及椭圆C1的方程;
(2)设圆C与y轴正半轴交于点D,O点为坐标原点,D,O中点为E,问是否存在直线l与椭圆C1交于M,N两点,且|ME|=|NE|?若存在,求出直线l与A1A2夹角θ的正切值的取值范围;若不存在,请说明理由.
【答案】分析:(1)先利用条件知道区域是直角三角形求出其外接圆C的方程,以及2a的值,再利用离心率即可求出椭圆C1的方程;
(2)把直线方程与椭圆C1的方程联立,求出M,N两点以及M,N中点与直线系数之间的关系,再把|ME|=|NE|转化为E在MN的中垂线上即可找到直线系数之间的等式,再代入前面求得的结论即可求出直线l与A1A2夹角θ的正切值的取值范围.
解答:解:(1)由题意可知,区域是以A1(-2,0),A2(2,0)及点 为顶点的三角形,
为顶点的三角形,
∵A1M⊥A2M,∴△A1A2M为直角三角形.(2分)
∴外接圆C以原点O为圆心,线段A1A2为直径,故其方程为x2+y2=4.
∵2a=4,∴a=2.
又 ,∴
,∴ ,可得
,可得 .
.
∴所求椭圆C1的方程是 .(6分)
.(6分)
(2)点D坐标为(0,2),故点E坐标为(0,1),显然θ=0可满足要求; 时不满足题意.(8分)
时不满足题意.(8分)
当 时,设l的方程为y=kx+m(k≠0),
时,设l的方程为y=kx+m(k≠0),
由 ,得(1+2k2)x2+4kmx+2m2-4=0,
,得(1+2k2)x2+4kmx+2m2-4=0,
由△=16k2m2-4(1+2k2)(2m2-4)>0,得4k2+2>m2;(10分)
设M(x1,y1),N(x2,y2),MN的中点为F(x,y),
则 .
.
∵ ,
,
即 ,
,
解得m=-1-2k2.(12分)
∴4k2+2>(-1-2k2)2,得 .
.
综上,直线l与A1A2夹角θ的正切值的取值范围是 .(14分)
.(14分)
点评:圆锥曲线的综合大题,主要考查解析几何的有关知识,以及分析问题与解决问题的能力.值得引起重视的一个现象是,经常出现一条或几条直线与两种圆锥曲线(包括圆)的位置关系问题,同时要注意其与平面几何、平面向量以及导数的知识的综合命题.
(2)把直线方程与椭圆C1的方程联立,求出M,N两点以及M,N中点与直线系数之间的关系,再把|ME|=|NE|转化为E在MN的中垂线上即可找到直线系数之间的等式,再代入前面求得的结论即可求出直线l与A1A2夹角θ的正切值的取值范围.
解答:解:(1)由题意可知,区域是以A1(-2,0),A2(2,0)及点
 为顶点的三角形,
为顶点的三角形,∵A1M⊥A2M,∴△A1A2M为直角三角形.(2分)
∴外接圆C以原点O为圆心,线段A1A2为直径,故其方程为x2+y2=4.
∵2a=4,∴a=2.
又
 ,∴
,∴ ,可得
,可得 .
.∴所求椭圆C1的方程是
 .(6分)
.(6分)(2)点D坐标为(0,2),故点E坐标为(0,1),显然θ=0可满足要求;
 时不满足题意.(8分)
时不满足题意.(8分)当
 时,设l的方程为y=kx+m(k≠0),
时,设l的方程为y=kx+m(k≠0),由
 ,得(1+2k2)x2+4kmx+2m2-4=0,
,得(1+2k2)x2+4kmx+2m2-4=0,由△=16k2m2-4(1+2k2)(2m2-4)>0,得4k2+2>m2;(10分)
设M(x1,y1),N(x2,y2),MN的中点为F(x,y),
则
 .
.∵
 ,
,即
 ,
,解得m=-1-2k2.(12分)
∴4k2+2>(-1-2k2)2,得
 .
.综上,直线l与A1A2夹角θ的正切值的取值范围是
 .(14分)
.(14分)点评:圆锥曲线的综合大题,主要考查解析几何的有关知识,以及分析问题与解决问题的能力.值得引起重视的一个现象是,经常出现一条或几条直线与两种圆锥曲线(包括圆)的位置关系问题,同时要注意其与平面几何、平面向量以及导数的知识的综合命题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率 .
.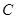 与
与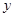 轴正半轴交于点D,
轴正半轴交于点D, 点为坐标原点,
点为坐标原点,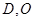 中点为
中点为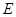 ,问是否存在直线
,问是否存在直线 与椭圆
与椭圆 交于
交于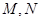 两点,且
两点,且 ?若存在,求出直线
?若存在,求出直线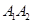 夹角
夹角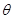 的正切值的取值范围;若不存在,请说明理由.
的正切值的取值范围;若不存在,请说明理由.
 (t为参数),求直线l被曲线C截得的线段长度.
(t为参数),求直线l被曲线C截得的线段长度. .
.