题目内容
已知函数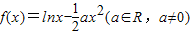 .
.(I)求函数f(x)的单调区间;
(II)已知点
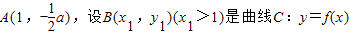 图角上的点,曲线C上是否存在点M(x,y)满足:①
图角上的点,曲线C上是否存在点M(x,y)满足:①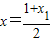 ;②曲线C在点M处的切线平行于直线AB?请说明理由.
;②曲线C在点M处的切线平行于直线AB?请说明理由.
【答案】分析:(I)f(x)的定义域是(0,+∞),对f(x)进行求导,利用导数研究函数f(x)的单调区间;
(II)假设存在满足条件的点M,根据A在曲线C上,求出直线AB的斜率,根据导数与斜率的关系KAB=f′(x),对其进行化简,从而进行判断;
解答:解:(I)f(x)的定义域是(0,+∞),
f′(x)=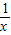 -ax=
-ax=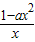 ,
,
①当a<0时,f′(x)>0,f(x)在(0,+∞)上单调递减,
当a>0时,由f′(x)>0和x>0得0<x<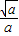
f(x)在(0,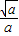 )内单调递增,
)内单调递增,
由f′(x)<0和x>0得x>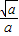 ,f(x)在(
,f(x)在(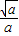 ,+∞)内单调递减,
,+∞)内单调递减,
综上所述:当a>0时,f(x)的单调增区间是(0,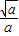 ),单调递减区间是(
),单调递减区间是(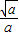 ,+∞);
,+∞);
(II)假设存在满足条件的点M,
∵A在曲线C上,∴KAB=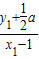 =
=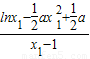 ,
,
f′(x)=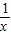 -ax,
-ax,
∴f′(x)=f′(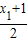 )=
)=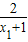 -a•
-a•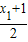 ,由已知KAB=f′(x),
,由已知KAB=f′(x),
∴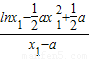 =
=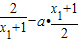 ,
,
化简整理可得lnx1=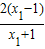 =2-
=2-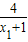 ,
,
即lnx1+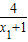 >2
>2
∴lnx1+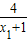 >2
>2
∴lnx1=2-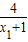 不成立,即满足条件的点M是不存在的;
不成立,即满足条件的点M是不存在的;
点评:此题主要考查利用导数研究函数的单调性,以及导数与斜率的关系,第二问是存在性问题,难度有些大,此题是一道中档题;
(II)假设存在满足条件的点M,根据A在曲线C上,求出直线AB的斜率,根据导数与斜率的关系KAB=f′(x),对其进行化简,从而进行判断;
解答:解:(I)f(x)的定义域是(0,+∞),
f′(x)=
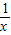 -ax=
-ax=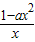 ,
,①当a<0时,f′(x)>0,f(x)在(0,+∞)上单调递减,
当a>0时,由f′(x)>0和x>0得0<x<
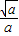
f(x)在(0,
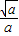 )内单调递增,
)内单调递增,由f′(x)<0和x>0得x>
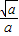 ,f(x)在(
,f(x)在(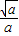 ,+∞)内单调递减,
,+∞)内单调递减,综上所述:当a>0时,f(x)的单调增区间是(0,
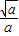 ),单调递减区间是(
),单调递减区间是(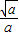 ,+∞);
,+∞);(II)假设存在满足条件的点M,
∵A在曲线C上,∴KAB=
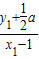 =
=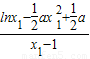 ,
,f′(x)=
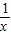 -ax,
-ax,∴f′(x)=f′(
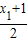 )=
)=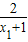 -a•
-a•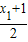 ,由已知KAB=f′(x),
,由已知KAB=f′(x),∴
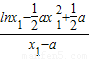 =
=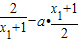 ,
,化简整理可得lnx1=
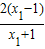 =2-
=2-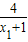 ,
,即lnx1+
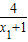 >2
>2∴lnx1+
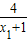 >2
>2∴lnx1=2-
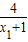 不成立,即满足条件的点M是不存在的;
不成立,即满足条件的点M是不存在的;点评:此题主要考查利用导数研究函数的单调性,以及导数与斜率的关系,第二问是存在性问题,难度有些大,此题是一道中档题;

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 的 部 分 图 象如 图 所示.
的 部 分 图 象如 图 所示. 的
解 析 式;
的
解 析 式; 中,角
中,角 的
对 边 分 别 是
的
对 边 分 别 是 ,若
,若 的
取 值 范 围.
的
取 值 范 围.