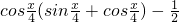题目内容
设函数y=f（x）满足：①y=f（x+1）是偶函数；②在[1，+∞）上为增函数，则f（-1）与f（2）的大小关系是________．
解：∵函数f（x）在（1，+∞）上为单调增函数
函数f（x+1）是偶函数，
∴f（-x+1）=f（x+1）
即函数f（x）的图象关于x=1对称
∴f （-1）=f（ 3），
根据函数f（x）在（1，+∞）上为单调增函数
∴f（2）＜f（ 3），即f（-1）＞f（2）
故答案为：f（-1）＞f（2）．
分析：根据函数f（x）在（1，+∞）上的单调性，以及函数f（x+1）是偶函数，将f （-1）化成f（ 3），利用单调性即可判定出f（-1）与f（2）的大小
点评：本题主要考查了函数的单调性应用，以及函数的奇偶性的应用，属于基础题．
函数f（x+1）是偶函数，
∴f（-x+1）=f（x+1）
即函数f（x）的图象关于x=1对称
∴f （-1）=f（ 3），
根据函数f（x）在（1，+∞）上为单调增函数
∴f（2）＜f（ 3），即f（-1）＞f（2）
故答案为：f（-1）＞f（2）．
分析：根据函数f（x）在（1，+∞）上的单调性，以及函数f（x+1）是偶函数，将f （-1）化成f（ 3），利用单调性即可判定出f（-1）与f（2）的大小
点评：本题主要考查了函数的单调性应用，以及函数的奇偶性的应用，属于基础题．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
