题目内容
将一颗骰子抛掷两次分别得到向上的点数
，
，则直线与圆相切的概率为（ ）
A． | B． | C． | D． |
B
解析试题分析：实验的总结果，
数对共有36种，直线与圆相切，得
，得
，即
，则数对共有
三种，故
，选B.
考点： 直线与圆相切条件、古典概率.
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
从装有
只红球和只黒球的口袋内任取个球，那么互斥而不对立的两个事件是( )
| A．至少有一个黒球与都是黒球 | B．至少有一个黒球与都是红球 |
C．至少有一个黒球与至少有 只红球 | D．恰有只黒球与恰有只黒球 |
连续抛掷两次骰子，得到的点数分别为m,n，记向量
的夹角为
，则
的概率是（ ）
A． | B． | C． | D． |
在面积为1的正方形
内部随机取一点
，则
的面积大于等于
的概率是（ ）
A． | B． | C． | D． |
在区域D：
内随机取一个点，则此点到点A(1，2)的距离大于2的概率是（ ）
A． | B． | C． | D． |
，若从区间
内随机选取一个实数
,则所选取的实数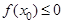
的概率为 （ ）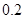
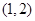内随机取个实数
，则直线
，直线
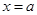与
轴围成的面积大于
的概率是（ ）
