题目内容
已知A、B、C是直线l上的三点,向量 、
、 、
、 满足:
满足: -(y+1-lnx)
-(y+1-lnx) +
+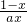
 =
= ,(O不在直线l上,a>0)
,(O不在直线l上,a>0)
(1)求y=f(x)的表达式;
(2)若函数f(x)在[1,+∞)上为增函数,求a的范围;
(3)求证:lnn> +
+ +
+ +…+
+…+ 对n≥2的正整数n恒成立.
对n≥2的正整数n恒成立.
解:(1)由已知得: =(y+1-lnx)
=(y+1-lnx)  +
+
 ,由A、B、C共线得:
,由A、B、C共线得:
y+1-lnx+ =1,整理得:y=lnx+
=1,整理得:y=lnx+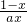
(2)f(x)=lnx+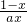 =lnx+
=lnx+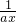 -
-
∴f′(x)= -
- ≥0在x∈[1,+∞)上恒成立
≥0在x∈[1,+∞)上恒成立
∴a≥ 在x∈[1,+∞)上的最大值,又
在x∈[1,+∞)上的最大值,又 ≤1
≤1
∴a≥1
证明:(3)当a=1时,f(x)=lnx+ -1
-1
由(2)知当x∈[1,+∞)时,f(x)=lnx+ -1≥f(1)=0
-1≥f(1)=0
∴lnx≥1- (仅x=1时取“=”)
(仅x=1时取“=”)
令x= 得:ln
得:ln >1-
>1- ,即:ln
,即:ln >
>
∴ln +ln
+ln +ln
+ln +…+ln
+…+ln >
> +
+ +
+ +…+
+…+
分析:(1)根据三点共线的充要条件,可得y+1-lnx+ =1,整理可得y=f(x)的表达式;
=1,整理可得y=f(x)的表达式;
(2)若函数f(x)在[1,+∞)上为增函数,则f′(x)≥0在x∈[1,+∞)上恒成立,进而求出a的范围;
(3)当a=1时,f(x)=lnx+ -1,结合(2)中函数的单调性,可得lnx≥1-
-1,结合(2)中函数的单调性,可得lnx≥1- ,令x=
,令x= 得:ln
得:ln >
> ,进而利用对数的运算性质,可证得结论.
,进而利用对数的运算性质,可证得结论.
点评:本题考查的知识点是不等式的证明,函数解析式的求法,导数法求函数的单调性,是函数与不等式问题的综合应用,难度较大.
 =(y+1-lnx)
=(y+1-lnx)  +
+
 ,由A、B、C共线得:
,由A、B、C共线得:y+1-lnx+
 =1,整理得:y=lnx+
=1,整理得:y=lnx+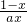
(2)f(x)=lnx+
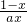 =lnx+
=lnx+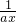 -
-
∴f′(x)=
 -
- ≥0在x∈[1,+∞)上恒成立
≥0在x∈[1,+∞)上恒成立∴a≥
 在x∈[1,+∞)上的最大值,又
在x∈[1,+∞)上的最大值,又 ≤1
≤1∴a≥1
证明:(3)当a=1时,f(x)=lnx+
 -1
-1由(2)知当x∈[1,+∞)时,f(x)=lnx+
 -1≥f(1)=0
-1≥f(1)=0∴lnx≥1-
 (仅x=1时取“=”)
(仅x=1时取“=”)令x=
 得:ln
得:ln >1-
>1- ,即:ln
,即:ln >
>
∴ln
 +ln
+ln +ln
+ln +…+ln
+…+ln >
> +
+ +
+ +…+
+…+
分析:(1)根据三点共线的充要条件,可得y+1-lnx+
 =1,整理可得y=f(x)的表达式;
=1,整理可得y=f(x)的表达式;(2)若函数f(x)在[1,+∞)上为增函数,则f′(x)≥0在x∈[1,+∞)上恒成立,进而求出a的范围;
(3)当a=1时,f(x)=lnx+
 -1,结合(2)中函数的单调性,可得lnx≥1-
-1,结合(2)中函数的单调性,可得lnx≥1- ,令x=
,令x= 得:ln
得:ln >
> ,进而利用对数的运算性质,可证得结论.
,进而利用对数的运算性质,可证得结论.点评:本题考查的知识点是不等式的证明,函数解析式的求法,导数法求函数的单调性,是函数与不等式问题的综合应用,难度较大.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目