题目内容
已知关于x的不等式:
(Ⅰ)若a=3,解该不等式;
(Ⅱ)若a>0,解该不等式.
解:(Ⅰ)当a=3时,原不等式即: ,即
,即 ,
,
即(2x-1)(x-1)>0,解得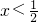 或x>1. 故解集为{ x|
或x>1. 故解集为{ x|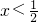 或x>1}. …(4分)
或x>1}. …(4分)
(Ⅱ)当a>0时,原不等式可化为: ,
,
(1)若a=1时,原不等式即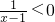 ,不等式的解集为{x|x<1}. …(5分)
,不等式的解集为{x|x<1}. …(5分)
(2)若a>1时,原不等式可化为 ,即 (x-
,即 (x- )(x-1)>0,
)(x-1)>0,
故①当1<a<2时,有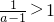 ,原不等式的解集为
,原不等式的解集为 .
.
②当a=2时,原不等式即 ,不等式的解集为{x|x≠1}.
,不等式的解集为{x|x≠1}.
③当a>2时,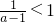 ,原不等式的解集为
,原不等式的解集为 .…(10分)
.…(10分)
(3)当1>a>0时,原不等式 可化为
可化为  ,
,
即 (x- )(x-1)<0,由于
)(x-1)<0,由于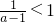 ,
,
故原不等式的解集为 .
.
分析:(Ⅰ)当a=3时,原不等式即: ,即
,即 ,由此解得x的范围.
,由此解得x的范围.
(Ⅱ)当a>0时,原不等式可化为(x- )•(x-1)>0.当a=1时,易求其解集;当a>1时,根据
)•(x-1)>0.当a=1时,易求其解集;当a>1时,根据 大于1、
大于1、
等于1、小于1三种情况,分别求出原不等式的解集.
点评:本题主要考查分式不等式,体现分类讨论与转化的数学思想,注意分类的层次,属于中档题.
 ,即
,即 ,
,即(2x-1)(x-1)>0,解得
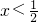 或x>1. 故解集为{ x|
或x>1. 故解集为{ x|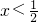 或x>1}. …(4分)
或x>1}. …(4分)(Ⅱ)当a>0时,原不等式可化为:
 ,
,(1)若a=1时,原不等式即
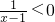 ,不等式的解集为{x|x<1}. …(5分)
,不等式的解集为{x|x<1}. …(5分)(2)若a>1时,原不等式可化为
 ,即 (x-
,即 (x- )(x-1)>0,
)(x-1)>0,故①当1<a<2时,有
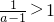 ,原不等式的解集为
,原不等式的解集为 .
.②当a=2时,原不等式即
 ,不等式的解集为{x|x≠1}.
,不等式的解集为{x|x≠1}.③当a>2时,
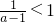 ,原不等式的解集为
,原不等式的解集为 .…(10分)
.…(10分)(3)当1>a>0时,原不等式
 可化为
可化为  ,
,即 (x-
 )(x-1)<0,由于
)(x-1)<0,由于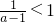 ,
,故原不等式的解集为
 .
.分析:(Ⅰ)当a=3时,原不等式即:
 ,即
,即 ,由此解得x的范围.
,由此解得x的范围.(Ⅱ)当a>0时,原不等式可化为(x-
 )•(x-1)>0.当a=1时,易求其解集;当a>1时,根据
)•(x-1)>0.当a=1时,易求其解集;当a>1时,根据 大于1、
大于1、等于1、小于1三种情况,分别求出原不等式的解集.
点评:本题主要考查分式不等式,体现分类讨论与转化的数学思想,注意分类的层次,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.