题目内容
已知函数f(x)= ,其中
,其中 cosωx),
cosωx), (ω>0),若f(x)图象中相邻对称轴间的距离为
(ω>0),若f(x)图象中相邻对称轴间的距离为 .
.
(1)求函数y=f(x)的单调递增区间;
(2)若函数g(x)=f(x)-a在区间[- ]上恰有两个零点,求a的取值范围.
]上恰有两个零点,求a的取值范围.
解:(1)∵ ,
,
f(x)图象中相邻对称轴间的距离为 ,∴T=π,∴w=1.
,∴T=π,∴w=1.
∴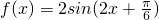 ,由 2kπ-
,由 2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,可得 kπ-
,可得 kπ- ≤x≤kπ+
≤x≤kπ+ ,
,
∴函数f(x)的增区间为: .
.
(2)∵ 在
在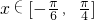 上恰有两个零点,
上恰有两个零点,
且 ,可知:a的取值范围是:
,可知:a的取值范围是: .
.
分析:(1)利用两角和正弦公式化简函数f(x)的解析式,根据周期求出w=1,由 2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,求出
,求出
x的范围,即为函数f(x)的增区间.
(2)由题意可得 ,解可得答案.
,解可得答案.
点评:本题考查两角和正弦公式,正弦函数的单调性,周期性,函数的零点的定义,求出函数f(x)的解析式,是解题的关键.
 ,
,f(x)图象中相邻对称轴间的距离为
 ,∴T=π,∴w=1.
,∴T=π,∴w=1.∴
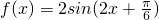 ,由 2kπ-
,由 2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,可得 kπ-
,可得 kπ- ≤x≤kπ+
≤x≤kπ+ ,
,∴函数f(x)的增区间为:
 .
.(2)∵
 在
在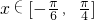 上恰有两个零点,
上恰有两个零点,且
 ,可知:a的取值范围是:
,可知:a的取值范围是: .
.分析:(1)利用两角和正弦公式化简函数f(x)的解析式,根据周期求出w=1,由 2kπ-
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,求出
,求出x的范围,即为函数f(x)的增区间.
(2)由题意可得
 ,解可得答案.
,解可得答案.点评:本题考查两角和正弦公式,正弦函数的单调性,周期性,函数的零点的定义,求出函数f(x)的解析式,是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|