题目内容
等差数列{an}、{bn}的前n项和分别为Sn和Tn,若A.1 B.![]() C.
C.![]() D.
D.![]()
分析:本题考查当n→∞时数列的极限.解题的关键是把结论中通项的比值用条件中前n项和的比值表示出来,即把![]() 转化成关于n的多项式.
转化成关于n的多项式.
解法一 设Sn=kn·2n,Tn=kn(3n+1)(k为非零常数).
由an=Sn-Sn-1(n≥2),
得an=2kn2-2k(n-1)2=4kn-2k,
bn=kn(3n+1)-k(n-1)[3(n-1)+1]=6kn-2k.
∴![]() =
=![]()
![]()
解法二 ∵![]() =
=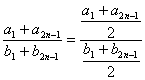
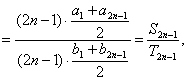
又∵![]()
∴![]()
∴![]()
答案:C

练习册系列答案
相关题目