题目内容
数列{an}的通项公式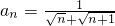 ,其前n项和时Sn=9,则n等于________.
,其前n项和时Sn=9,则n等于________.
99
分析:根据题意,数列的通项公式可转化an= -
- ,进而可得Sn=(
,进而可得Sn=( -
- )-(
)-( -
-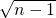 )+…+(
)+…+( -1)=
-1)= -1,已知Sn=9,即
-1,已知Sn=9,即 -1=9,解可得答案.
-1=9,解可得答案.
解答:根据题意,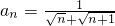 =
= -
- ,
,
则Sn=( -
- )-(
)-( -
-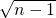 )+…+(
)+…+( -1)=
-1)= -1,
-1,
若Sn=9,即 -1=9,
-1=9,
解可得n=99;
故答案为99.
点评:本题考查数列的求和,解本题的关键在于数列的通项公式的转化,即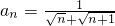 =
= -
- ,进而化简得到前n项和的表达式.
,进而化简得到前n项和的表达式.
分析:根据题意,数列的通项公式可转化an=
 -
- ,进而可得Sn=(
,进而可得Sn=( -
- )-(
)-( -
-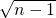 )+…+(
)+…+( -1)=
-1)= -1,已知Sn=9,即
-1,已知Sn=9,即 -1=9,解可得答案.
-1=9,解可得答案.解答:根据题意,
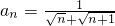 =
= -
- ,
,则Sn=(
 -
- )-(
)-( -
-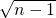 )+…+(
)+…+( -1)=
-1)= -1,
-1,若Sn=9,即
 -1=9,
-1=9,解可得n=99;
故答案为99.
点评:本题考查数列的求和,解本题的关键在于数列的通项公式的转化,即
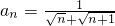 =
= -
- ,进而化简得到前n项和的表达式.
,进而化简得到前n项和的表达式. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,Tn为数列{bn}的前n项和,求Tn.
,Tn为数列{bn}的前n项和,求Tn.