题目内容
设奇函数 上是增函数,且
上是增函数,且 ,则不等式
,则不等式 的解集为( )
的解集为( )
A.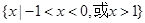 | B.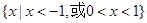 |
C. | D. |
D
解析试题分析:由题意可知,函数f(x)是奇函数,函数f(x)在(0,+∞)上是增函数,∴它在(-∞,0)上也是增函数.∵f(-x)=-f(x),∴f(-1)=f(1)=0.不等式x[f(x)-f(-x)]<0可化为2xf(x)<0,即xf(x)<0,∴当x<0时,可得f(x)>0=f(-1),∴x>-1,∴-1<x<0;当x>0时,可得f(x)<0=f(1),∴x<1,∴0<x<1.综上,
不等式x[f(x)-f(-x)]<0的解集为{x|-1<x0,或0<x<1}.故选D.
考点:本试题主要考查了是函数的奇偶性和单调性以及解不等式的综合类问题.在解答的过程当中充分体现了转化的思想、数形结合的思想以及函数单调性与奇偶性的知识.值得同学们体会和反思.
点评:解决该试题的关键要结合奇偶性和单调性对不等式进行转化变形,将问题转化为解不等式:2xf(x)<0,然后再分类讨论即可获得问题的解答。

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
下列四个函数中,在 上为增函数的是( )
上为增函数的是( )
A. | B. | C. | D. |
对实数a和b,定义运算“⊕”:a⊕b= 设函数f(x)=(x2-2)⊕(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
设函数f(x)=(x2-2)⊕(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
A.(-∞,-2]∪ | B.(-∞,-2]∪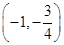 |
C.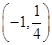 ∪ ∪ | D.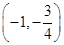 ∪ ∪ |
下列各组函数中,表示同一个函数的是( )
A. , , | B. , , |
C. , , | D. , , |
设 是
是 上的任意函数,则下列叙述正确的是( )
上的任意函数,则下列叙述正确的是( )
A. 是奇函数 是奇函数 | B. 是奇函数 是奇函数 |
C. 是偶函数 是偶函数 | D. 是偶函数 是偶函数 |
 是
是 上的奇函数,当
上的奇函数,当 时,
时, ;则当
;则当 时,
时, 等于
等于
A. | B. | C. | D. |


 与奇函数
与奇函数 的定义域都是
的定义域都是 ,它们在
,它们在 上的图象分别为图(1)、(2)所示,则使关于
上的图象分别为图(1)、(2)所示,则使关于 的不等式
的不等式 成立的
成立的



