题目内容
【题目】某地拟建造一座大型体育馆,其设计方案侧面的外轮廓如图所示,曲线![]() 是以点
是以点![]() 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中![]() ;曲线
;曲线![]() 是抛物线
是抛物线![]() 的一部分;
的一部分;![]() ,且
,且![]() 恰好等于圆
恰好等于圆![]() 的半径.假定拟建体育馆的高
的半径.假定拟建体育馆的高![]() (单位:米,下同).
(单位:米,下同).
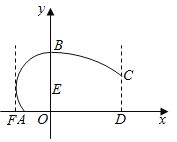
(1)若![]() ,
,![]() ,求
,求![]() 、
、![]() 的长度;
的长度;
(2)若要求体育馆侧面的最大宽度![]() 不超过
不超过![]() 米,求
米,求![]() 的取值范围;
的取值范围;
(3)若![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 米.
米.
【解析】
(1)由![]() 可求出
可求出![]() 的长,在抛物线方程中,令
的长,在抛物线方程中,令![]() ,可求出
,可求出![]() 的长,在圆
的长,在圆![]() 的方程中,令
的方程中,令![]() ,可求出
,可求出![]() 的长,相加即可得出
的长,相加即可得出![]() 的长;
的长;
(2)问题转化为![]() 恒成立,根据基本不等式解出即可;
恒成立,根据基本不等式解出即可;
(3)先求得![]() ,在圆
,在圆![]() 的方程中,令
的方程中,令![]() ,可得出
,可得出![]() ,从而得出
,从而得出![]() ,令
,令![]() ,将问题转化为求函数
,将问题转化为求函数![]() 在
在![]() 上的最大值.
上的最大值.
法一:令![]() ,
,![]() ,利用三角函数知识可求出
,利用三角函数知识可求出![]() 的最大值;
的最大值;
法二:令![]() ,
,![]() ,将问题转化为已知
,将问题转化为已知![]() ,求
,求![]() 的最大值,利用数形结合思想可求出
的最大值,利用数形结合思想可求出![]() 的最大值.
的最大值.
(1)因为圆![]() 的半径为
的半径为![]() ,所以
,所以![]() 米,
米,
在![]() 中令
中令![]() ,得
,得![]()
在圆![]() 中,令
中,令![]() 得
得![]() ,
,
所以![]() 米;
米;
(2)由圆![]() 的半径为
的半径为![]() ,得
,得![]()
在![]() 中,令
中,令![]() ,得
,得![]() ,
,![]()
由题意知![]() 对
对![]() 恒成立,所以
恒成立,所以![]() 恒成立.
恒成立.
当![]() 时,即当
时,即当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,故
,故![]() ,解得
,解得![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(3)当![]() 时,
时,![]()
又圆![]() 的方程为
的方程为![]() ,令
,令![]() ,得
,得![]() ,
,
所以![]() ,从而
,从而![]()
下求![]() 的最大值.
的最大值.
方法一:令![]() ,
,![]() ,
,
则![]() ,
,
其中![]() 是锐角,且
是锐角,且![]() ,从而当
,从而当![]() 时,
时,![]() 取得最大值
取得最大值![]() ;
;
方法二:令![]() ,
,![]() ,则题意相当于:已知
,则题意相当于:已知![]() ,求
,求![]() 的最大值.
的最大值.
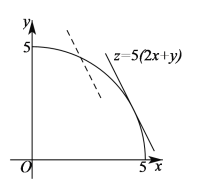
当直线![]() 与圆弧
与圆弧![]() 相切时,直线
相切时,直线![]() 在
在![]() 轴上的截距最大,此时
轴上的截距最大,此时![]() 取最大值,且有
取最大值,且有![]() ,
,![]() ,解得
,解得![]() ,
,
因此,![]() 的最大值为
的最大值为![]()
答:当![]() 米时,
米时,![]() 的最大值为
的最大值为![]() 米.
米.

练习册系列答案
相关题目