题目内容
已知函数 ,函数
,函数 .
.
(I)试求f(x)的单调区间。
(II)若f(x)在区间 上是单调递增函数,试求实数a的取值范围:
上是单调递增函数,试求实数a的取值范围:
(III)设数列 是公差为1.首项为l的等差数列,数列
是公差为1.首项为l的等差数列,数列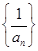 的前n项和为
的前n项和为 ,求证:当
,求证:当 时,
时,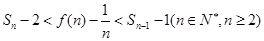 .
.
【答案】
(Ⅰ) 的单调递增区间是
的单调递增区间是 ;
; 的单调递减区间是
的单调递减区间是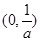 ;
;
(Ⅱ) .(Ⅲ)见解析.
.(Ⅲ)见解析.
【解析】
试题分析:(Ⅰ) 利用导数值非负,得 的单调递增区间是
的单调递增区间是 ;利用导数值非正,得到
;利用导数值非正,得到 的单调递减区间是
的单调递减区间是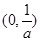 ;
;
(Ⅱ)利用 在
在 是单调递增函数,则
是单调递增函数,则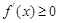 恒成立,只需
恒成立,只需 恒成立,转化成
恒成立,转化成
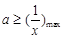 ,利用
,利用 ,得到
,得到 .
.
(Ⅲ)依题意不难得到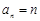 ,
, =1+
=1+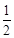 ++
++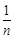 ,
,
根据 时,
时,
 =
= +
+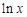 在
在 上为增函数,
上为增函数,
可得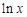

 ,从而
,从而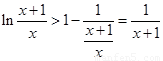 ;
;
构造函数 ,利用“导数法”得到
,利用“导数法”得到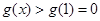 , 从而不等式
, 从而不等式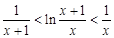 成立.
成立.
应用“累加法”证得不等式.
本题解答思路比较明确,考查方法较多,是一道相当典型的题目.
试题解析:(Ⅰ) =
=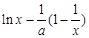 ,所以,
,所以,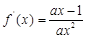 ,
,
因为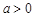 ,
,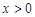 ,所以
,所以 ,令
,令 ,
, ,
,
所以 的单调递增区间是
的单调递增区间是 ;
; 的单调递减区间是
的单调递减区间是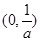 ;4分
;4分
(Ⅱ)若 在
在 是单调递增函数,则
是单调递增函数,则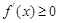 恒成立,即
恒成立,即 恒成立
恒成立
即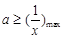 ,因为
,因为 ,所以
,所以 故
故 .
.7分
.
.7分
(Ⅲ)设数列 是公差为1首项为1的等差数列,所以
是公差为1首项为1的等差数列,所以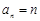 ,
, =1+
=1+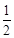 ++
++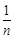 ,
,
当 时,由(Ⅱ)知:
时,由(Ⅱ)知: =
= +
+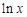 在
在 上为增函数,
上为增函数,
 =
=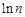 -1,当
-1,当 时,
时,

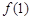 ,所以
,所以 +
+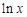
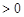 ,即
,即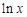


所以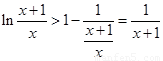 ;
;
令 ,则有
,则有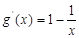 ,当
,当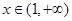 ,有
,有
则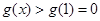 ,即
,即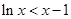 ,所以
,所以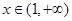 时,
时,
所以不等式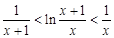 成立.
成立.
令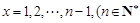 且
且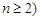 时,
时,
将所得各不等式相加,得
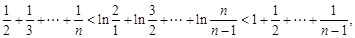
即
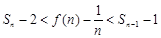 (
(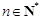 且
且 ).
13分
).
13分
考点:应用导数研究函数的单调性,等差数列的通项公式,“累加法”.

练习册系列答案
相关题目
 已知函数f(x)的定义域为[-2,+∞),部分对应值如表格所示,f′(x)为f(x).的导函数,函数y=f′(x)的图象如右图所示:
已知函数f(x)的定义域为[-2,+∞),部分对应值如表格所示,f′(x)为f(x).的导函数,函数y=f′(x)的图象如右图所示: