题目内容
 设函数f(x)=x2-4|x|-5.
设函数f(x)=x2-4|x|-5.(Ⅰ)画出y=f(x)的图象;
(Ⅱ)设A={x|f(x)≥7},求集合A;
(Ⅲ)方程f(x)=k+1有两解,求实数k的取值范围.
分析:(Ⅰ)根据函数f(x)=x2-4|x|-5=
,画出y=f(x)的图象,如图.
(Ⅱ)由f(x)≥7可得 即 ①
,或②
.分别求得①、②的解集额,再取并集,即得所求.
(Ⅲ)方程f(x)=k+1有两解,即函数f(x)的图象和直线y=k+1有两个不同的交点,结合函数f(x)的图象可得k的范围.
|
(Ⅱ)由f(x)≥7可得 即 ①
|
|
(Ⅲ)方程f(x)=k+1有两解,即函数f(x)的图象和直线y=k+1有两个不同的交点,结合函数f(x)的图象可得k的范围.
解答: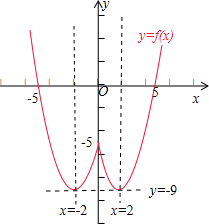 解:(Ⅰ)∵函数f(x)=x2-4|x|-5=
解:(Ⅰ)∵函数f(x)=x2-4|x|-5=
,画出y=f(x)的图象,如图:
(Ⅱ)由f(x)≥7可得 x2-4|x|-5≥7,
即 ①
,或②
.
解①得x≥6,解②可得 x≤-6,
故A={x|f(x)≥7}=(-∞,-6]∪[6,+∞).
(Ⅲ)方程f(x)=k+1有两解,即函数f(x)的图象和直线y=k+1有两个不同的交点,
由于当x=±2时,函数f(x)取得最小值为-9,
结合函数f(x)的图象可得k+1=-9,或 k+1>-5,
解得k=-10,或k>-6,
即k的范围为{-10}∪(-6,+∞).
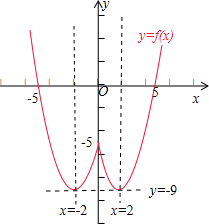 解:(Ⅰ)∵函数f(x)=x2-4|x|-5=
解:(Ⅰ)∵函数f(x)=x2-4|x|-5=
|
(Ⅱ)由f(x)≥7可得 x2-4|x|-5≥7,
即 ①
|
|
解①得x≥6,解②可得 x≤-6,
故A={x|f(x)≥7}=(-∞,-6]∪[6,+∞).
(Ⅲ)方程f(x)=k+1有两解,即函数f(x)的图象和直线y=k+1有两个不同的交点,
由于当x=±2时,函数f(x)取得最小值为-9,
结合函数f(x)的图象可得k+1=-9,或 k+1>-5,
解得k=-10,或k>-6,
即k的范围为{-10}∪(-6,+∞).
点评:本题主要考查作函数的图象,函数的零点与方程的根的关系,绝对值不等式的解法,体现了数形结合、转化的数学思想,属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目